Opis ruchu w fizyce to nic innego jak próba zrozumienia i wyrażenia, w jaki sposób obiekty zmieniają swoje położenie w przestrzeni i czasie. Dla każdego, kto rozpoczyna swoją przygodę z fizyką, a w szczególności dla uczniów szkół średnich, opanowanie podstawowych pojęć kinematyki jest absolutnie kluczowe. Bez tego solidnego fundamentu trudno będzie budować dalszą wiedzę o świecie.
Opis ruchu w fizyce kluczowe pojęcia kinematyki dla początkujących
- Ruch i spoczynek są względne, a ich opis wymaga zawsze zdefiniowania układu odniesienia.
- Podstawowe wielkości to tor ruchu, droga (skalar) oraz przemieszczenie (wektor).
- Szybkość to wartość skalarna, a prędkość to wektor, który oprócz wartości określa także kierunek i zwrot ruchu.
- Przyspieszenie to zmiana prędkości w czasie, odpowiadająca za ruchy przyspieszone i opóźnione.
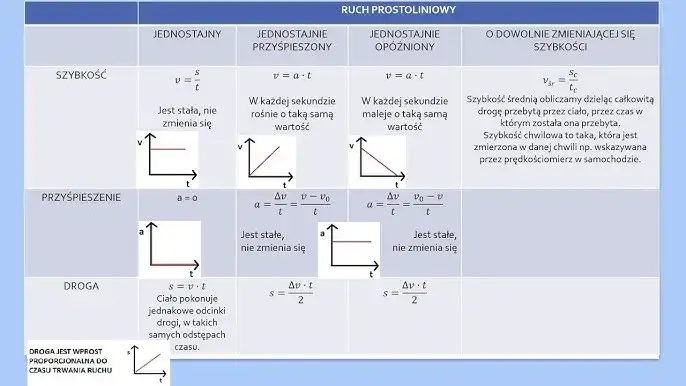
- Ruchy dzielimy na jednostajne i jednostajnie zmienne, każdy z nich opisują konkretne wzory.
- Umiejętność czytania i interpretacji wykresów kinematycznych jest niezbędna do wizualizacji i analizy ruchu.
Względność ruchu: Dlaczego układ odniesienia jest niezbędny?
Czym jest ruch, a czym spoczynek w oczach fizyka?
Zacznijmy od fundamentalnego pytania: czym właściwie jest ruch? W fizyce ruch i spoczynek to pojęcia, które zawsze musimy rozpatrywać w kontekście czegoś innego. Mówiąc prościej, są one względne. To, co dla jednego obserwatora jest w ruchu, dla innego może być w spoczynku. Wyobraź sobie drzewo. Dla osoby stojącej na ziemi drzewo jest w spoczynku. Ale dla pasażera jadącego pociągiem z dużą prędkością, to samo drzewo "przesuwa się" obok, czyli jest w ruchu. To zjawisko jest kluczowe i często bywa źródłem nieporozumień na początku nauki.
Układ odniesienia: Twój niezbędny punkt startowy do opisu świata
Aby móc jednoznacznie opisać ruch jakiegokolwiek ciała, musimy zawsze określić, względem czego ten ruch się odbywa. I tu właśnie wkracza pojęcie układu odniesienia. Jest to absolutna podstawa i niezbędny punkt startowy dla każdego opisu ruchu. Bez zdefiniowania układu odniesienia, mówienie o ruchu czy spoczynku jest po prostu bezsensowne. To tak, jakbyś próbował podać komuś wskazówki dojazdu, nie mówiąc, skąd ma wyruszyć.
Praktyczne przykłady względności ruchu, które znasz z codziennego życia
Względność ruchu otacza nas na co dzień. Oto kilka przykładów, które pomogą ci to lepiej zrozumieć:
-
Pasażer w jadącym autobusie:
- Względem siedzenia w autobusie, pasażer jest w spoczynku.
- Względem latarni ulicznej na zewnątrz, pasażer jest w ruchu.
-
Słońce i Ziemia:
- Względem powierzchni Ziemi, domy są w spoczynku.
- Względem Słońca, te same domy (razem z całą Ziemią) są w ruchu z ogromną prędkością.
-
Samochód na autostradzie:
- Dla kierowcy jadącego obok z tą samą prędkością, drugi samochód może wydawać się w spoczynku (nie zmienia położenia względem niego).
- Dla obserwatora stojącego na moście nad autostradą, oba samochody są w ruchu.
Narzędzia fizyka: Jak opisać tor i położenie ciała?
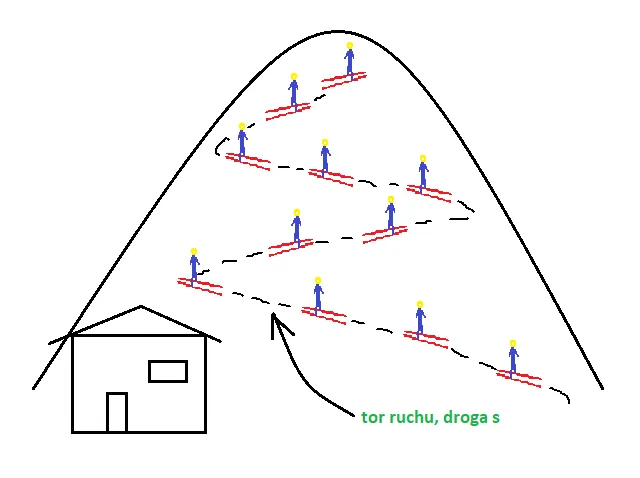
Tor ruchu: Ślad, który zostawia za sobą poruszające się ciało
Kiedy ciało się porusza, zostawia za sobą pewien "ślad" w przestrzeni. Ten ślad nazywamy torem ruchu. Tor ruchu to nic innego jak linia, którą zakreśla poruszające się ciało. Może to być linia prosta (mówimy wtedy o ruchu prostoliniowym) lub linia krzywa (ruch krzywoliniowy), na przykład okrąg w przypadku karuzeli czy parabola w przypadku rzutu ukośnego. Zrozumienie toru ruchu to pierwszy krok do precyzyjnego opisu przemieszczania się obiektów.
Droga (skalar): Ile faktycznie mierzysz kroków?
Gdy już wiemy, czym jest tor, możemy zdefiniować drogę (s). Droga to po prostu długość tego toru ruchu, czyli całkowita odległość, jaką ciało przebyło. Jest to wielkość skalarna, co oznacza, że ma tylko wartość (np. 100 metrów, 5 kilometrów) i nie ma kierunku ani zwrotu. Co ważne, droga zawsze jest wartością nieujemną nie możesz przebyć "ujemnej" drogi, a jeśli się poruszasz, droga zawsze rośnie.
Przemieszczenie (wektor): Gdzie jesteś względem punktu startowego?
W przeciwieństwie do drogi, przemieszczenie (Δr lub Δx) jest wielkością wektorową. Oznacza to, że ma nie tylko wartość, ale także kierunek i zwrot. Przemieszczenie to wektor, który łączy punkt początkowy ruchu z punktem końcowym. Mówi nam, gdzie ciało znalazło się względem swojego punktu startowego, niezależnie od tego, jaką drogę przebyło. Co ciekawe, przemieszczenie może być zerowe, nawet jeśli ciało przebyło znaczną drogę pomyśl o okrążeniu stadionu.
Droga a przemieszczenie kluczowa różnica, którą musisz zrozumieć raz na zawsze
Rozróżnienie między drogą a przemieszczeniem to jeden z najczęstszych problemów dla początkujących. Pozwól, że przedstawię to w tabeli, abyś raz na zawsze zapamiętał tę kluczową różnicę. Weźmy przykład sportowca, który przebiega pełne okrążenie stadionu o długości 400 metrów, startując i kończąc w tym samym miejscu.
| Cecha / Właściwość | Droga (s) | Przemieszczenie (Δr) |
|---|---|---|
| Definicja | Całkowita długość toru ruchu | Wektor łączący punkt początkowy z końcowym |
| Typ wielkości | Skalarna (tylko wartość) | Wektorowa (wartość, kierunek, zwrot) |
| Wartość | Zawsze nieujemna | Może być dodatnia, ujemna lub zerowa |
| Przykład (pełne okrążenie stadionu 400m) | 400 metrów | 0 metrów (wektor zerowy), bo punkt początkowy = punkt końcowy |
| Co mówi? | Jak dużo się poruszałeś | Gdzie jesteś względem startu |
Szybkość czy prędkość? Rozróżnij te kluczowe pojęcia
Szybkość: Jak odczytać ją z licznika w samochodzie?
W codziennym języku często używamy zamiennie słów "szybkość" i "prędkość", ale w fizyce to dwie różne wielkości! Szybkość (v) to wielkość skalarna, która mówi nam, jak szybko ciało się porusza. Definiujemy ją jako stosunek przebytej drogi do czasu, w jakim ta droga została pokonana. To właśnie szybkość odczytujesz z licznika w samochodzie pokazuje on tylko wartość, np. 50 km/h, bez informowania o tym, w którą stronę jedziesz.
Prędkość: Co oprócz wartości mówi nam ten wektor?
Natomiast prędkość (v⃗) to wielkość wektorowa. Oznacza to, że oprócz wartości (czyli szybkości), informuje nas także o kierunku i zwrocie ruchu. Prędkość definiujemy jako stosunek przemieszczenia do czasu. Jeśli mówię, że samochód jedzie z prędkością 50 km/h na północ, to podaję jego prędkość. Jeśli powiem tylko, że jedzie z szybkością 50 km/h, to nie wiem, czy jedzie na północ, południe, czy może skręca.
Prędkość średnia a chwilowa na czym polega różnica?
Warto również rozróżnić prędkość średnią od prędkości chwilowej. Prędkość średnia to całkowita droga podzielona przez całkowity czas (dla szybkości średniej) lub całkowite przemieszczenie podzielone przez całkowity czas (dla prędkości średniej). Jest to uśredniona wartość dla całego odcinka ruchu. Na przykład, jeśli przejechałeś 100 km w 2 godziny, Twoja średnia szybkość wynosiła 50 km/h. Jednak w trakcie tej podróży mogłeś jechać 30 km/h, potem 70 km/h, a na koniec stać w korku. Prędkość chwilowa to prędkość ciała w danej, konkretnej chwili. To właśnie ją pokazuje licznik w samochodzie w danym momencie. Moja rada: zawsze zwracaj uwagę na kontekst, aby wiedzieć, czy mowa o średniej, czy chwilowej wartości.
Gdy ruch nabiera tempa: Zrozumienie przyspieszenia
Definicja przyspieszenia: Co oznacza, że prędkość się zmienia?
Do tej pory omawialiśmy ruch, w którym prędkość mogła być stała. Ale co, jeśli prędkość się zmienia? Wtedy mówimy o przyspieszeniu (a⃗). Przyspieszenie to wielkość wektorowa, która mówi nam, jak szybko zmienia się prędkość ciała w jednostce czasu. Jeśli prędkość ciała wzrasta, mówimy o przyspieszeniu. Jeśli maleje, również mamy do czynienia z przyspieszeniem, ale o przeciwnym zwrocie.
Ruch przyspieszony i opóźniony kiedy wciskasz gaz, a kiedy hamujesz?
Wyobraź sobie jazdę samochodem. Kiedy wciskasz pedał gazu, samochód przyspiesza jego prędkość rośnie. W fizyce nazywamy to ruchem jednostajnie przyspieszonym, jeśli przyspieszenie jest stałe i zgodne ze zwrotem prędkości. Natomiast kiedy wciskasz pedał hamulca, samochód zwolnia, czyli jego prędkość maleje. To jest ruch jednostajnie opóźniony. W tym przypadku przyspieszenie jest również stałe, ale ma zwrot przeciwny do zwrotu prędkości. To proste analogie, które pomogą ci zrozumieć te kluczowe pojęcia.
Jak obliczyć przyspieszenie i jaką ma jednostkę?
Przyspieszenie obliczamy ze wzoru:
a = Δv/Δt
Gdzie:
- a to przyspieszenie,
- Δv to zmiana prędkości (prędkość końcowa minus prędkość początkowa),
- Δt to czas, w którym ta zmiana nastąpiła.
Klasyfikacja ruchów: Jednostajny i jednostajnie zmienny
Ruch jednostajny prostoliniowy: Spokojny spacer w stałym tempie
Najprostszym typem ruchu jest ruch jednostajny prostoliniowy. Jak sama nazwa wskazuje, tor tego ruchu jest linią prostą, a co najważniejsze, prędkość ma stałą wartość (i stały kierunek oraz zwrot). Oznacza to, że ciało pokonuje równe odcinki drogi w równych odstępach czasu. Wyobraź sobie kogoś, kto idzie spokojnym spacerem, zawsze w tym samym tempie i w linii prostej. Wzór na drogę w tym ruchu jest bardzo prosty: s = v * t, gdzie 's' to droga, 'v' to prędkość, a 't' to czas.
Ruch jednostajnie przyspieszony: Start rakiety i swobodne spadanie
Kiedy prędkość ciała się zmienia, mamy do czynienia z ruchem jednostajnie zmiennym. W tym przypadku tor również jest linią prostą, ale przyspieszenie ma stałą wartość. Jeśli przyspieszenie jest dodatnie i zgodne ze zwrotem prędkości, mówimy o ruchu jednostajnie przyspieszonym prędkość ciała rośnie liniowo z czasem (jak start rakiety). Jeśli przyspieszenie jest ujemne (czyli przeciwne do zwrotu prędkości), mamy ruch jednostajnie opóźniony (jak hamujący samochód). W ruchu jednostajnie zmiennym prędkość zmienia się liniowo, a droga rośnie kwadratowo z czasem. Klasycznym przykładem ruchu jednostajnie przyspieszonego jest swobodne spadanie ciał w polu grawitacyjnym.
Kluczowe wzory, które rządzą tymi ruchami Twoja ściągawka
Aby ułatwić ci zapamiętanie, zebrałem najważniejsze wzory opisujące ruchy jednostajny i jednostajnie zmienny:
-
Ruch jednostajny prostoliniowy:
- Droga: s = v * t
-
Ruch jednostajnie zmienny prostoliniowy (przyspieszony/opóźniony):
- Prędkość końcowa: vk = v0 + a * t (gdzie v0 to prędkość początkowa)
- Droga: s = v0 * t + (a * t2) / 2
Wykresy kinematyczne: Jak czytać ruch z grafów?
Wykres drogi od czasu (s(t)): Co zdradza nachylenie linii?
Wykresy są potężnym narzędziem w fizyce, pozwalającym wizualizować ruch. Wykres położenia od czasu (s(t) lub x(t)) pokazuje, jak zmienia się położenie ciała w zależności od upływającego czasu. Kluczową informacją, jaką możemy z niego odczytać, jest nachylenie linii. Im bardziej stroma jest linia, tym większa jest prędkość ciała. Linia pozioma oznacza, że ciało jest w spoczynku (prędkość zerowa), a linia prosta o stałym nachyleniu wskazuje na ruch jednostajny.
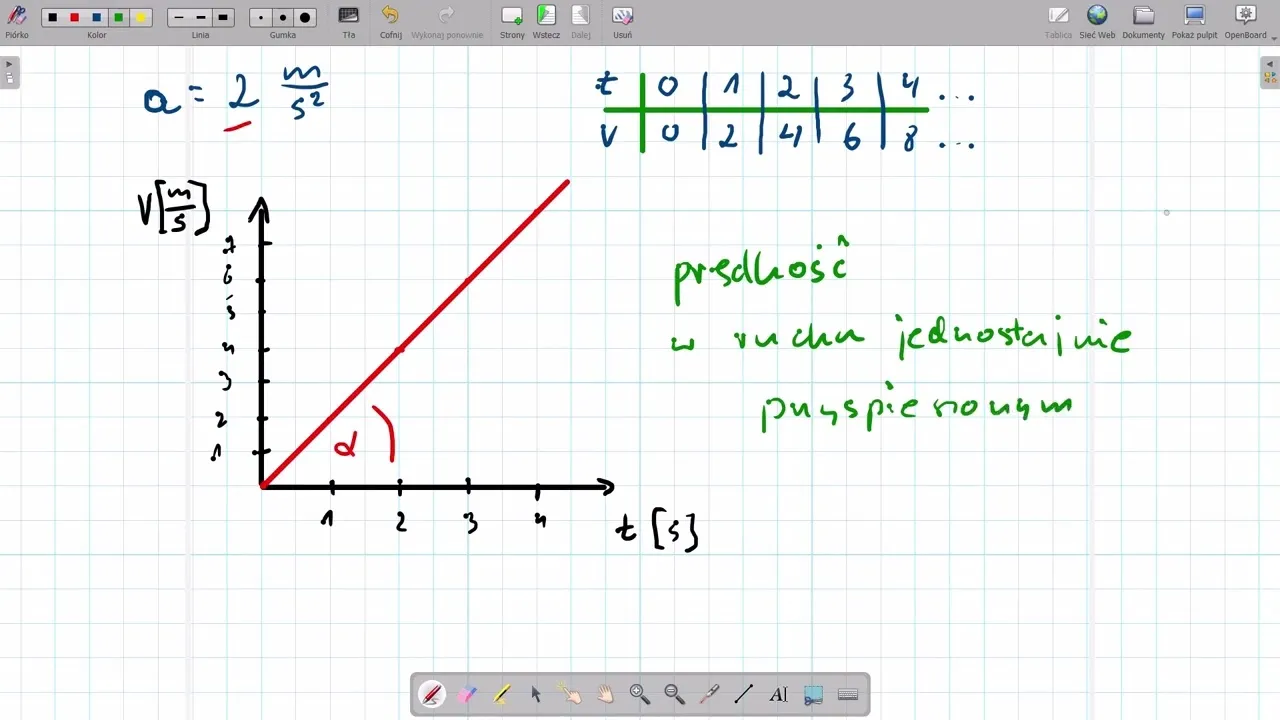
Wykres prędkości od czasu (v(t)): Odkryj tajemnice nachylenia i pola pod wykresem
Wykres prędkości od czasu (v(t)) dostarcza jeszcze więcej informacji. Tutaj również ważne jest nachylenie linii tym razem nachylenie linii odpowiada przyspieszeniu. Jeśli linia jest pozioma, przyspieszenie jest zerowe (ruch jednostajny). Jeśli linia jest prosta i nachylona, mamy ruch jednostajnie zmienny (przyspieszenie stałe). Co więcej, pole pod wykresem v(t) reprezentuje przebytą drogę. To bardzo przydatna właściwość, którą często wykorzystujemy do obliczeń.
Przeczytaj również: Co to jest wektor w fizyce? Zrozum cechy i zastosowania!
Wykres przyspieszenia od czasu (a(t)): Najprostszy obraz dla ruchów jednostajnie zmiennych
Na koniec mamy wykres przyspieszenia od czasu (a(t)). Jest on szczególnie prosty w interpretacji dla ruchów jednostajnie zmiennych. W takim przypadku, ponieważ przyspieszenie jest stałe, wykres a(t) będzie po prostu prostą poziomą, której wartość odpowiada wartości przyspieszenia. Jeśli przyspieszenie wynosi 0, linia będzie leżeć na osi czasu, co oznacza ruch jednostajny.
Podsumowanie: Opanuj język opisu ruchu w fizyce
Mam nadzieję, że ten artykuł pomógł ci uporządkować podstawowe pojęcia związane z opisem ruchu w fizyce. Zrozumienie względności ruchu i roli układu odniesienia, odróżnianie drogi od przemieszczenia oraz szybkości od prędkości, a także pojmowanie przyspieszenia jako zmiany prędkości, to absolutne fundamenty. Kiedy dodamy do tego znajomość klasyfikacji ruchów (jednostajny, jednostajnie zmienny) i umiejętność interpretacji wykresów kinematycznych, zyskujesz solidne narzędzia do analizy i przewidywania, jak obiekty poruszają się w naszym świecie. To język, który pozwoli ci zrozumieć znacznie bardziej złożone zjawiska fizyczne w przyszłości.