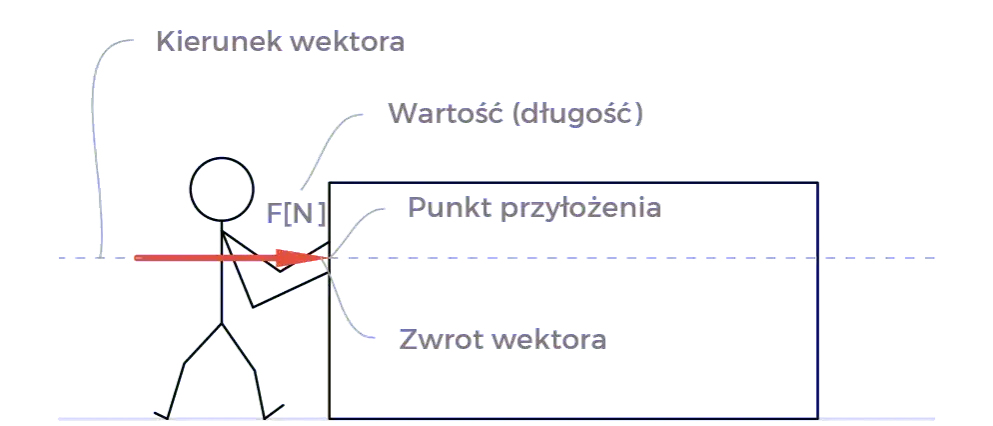
W świecie fizyki, gdzie precyzja opisu zjawisk jest kluczowa, nie zawsze wystarczy podać samą wartość liczbową. Wyobraźmy sobie, że mówimy o sile czy wystarczy powiedzieć, że działa siła 100 niutonów? Absolutnie nie! Musimy wiedzieć, w którą stronę ta siła działa, pod jakim kątem i w którym miejscu. Właśnie w takich sytuacjach na scenę wkraczają wektory matematyczne narzędzia, które pozwalają nam opisywać wielkości posiadające nie tylko wartość, ale i kierunek oraz zwrot. Zrozumienie wektorów jest fundamentalne dla każdego, kto chce zgłębić tajniki mechaniki i innych działów fizyki, ponieważ to one stanowią język, którym fizyka mówi o ruchu, oddziaływaniach i polach.
Wektor w fizyce klucz do opisu wielkości mających kierunek i zwrot
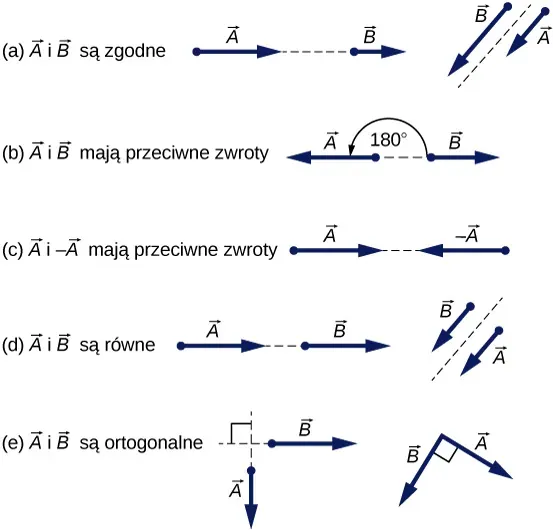
- Wektor to wielkość fizyczna posiadająca wartość liczbową oraz orientację w przestrzeni, przedstawiana graficznie jako strzałka.
- Do pełnego opisu wektora niezbędne są cztery cechy: wartość (moduł), kierunek, zwrot i punkt przyłożenia.
- Wektory różnią się od skalarów, które są opisywane wyłącznie przez wartość liczbową (np. masa, czas).
- Przykłady wektorów w fizyce to siła, prędkość, przyspieszenie, przemieszczenie i pęd.
- Na wektorach można wykonywać podstawowe operacje, takie jak dodawanie, odejmowanie i mnożenie przez skalar, co jest kluczowe w rozwiązywaniu zadań.
Wprowadzenie do świata wektorów: Kiedy sama wartość to za mało
Wektor to nic innego jak wielkość fizyczna, która do pełnego opisu wymaga podania nie tylko swojej wartości liczbowej, ale także kierunku i zwrotu. Najłatwiej wyobrazić go sobie jako strzałkę. Długość tej strzałki odpowiada wartości wielkości, linia, na której leży, określa kierunek, a grot wskazuje zwrot. Kiedy mówimy o prędkości samochodu, nie wystarczy powiedzieć "jedzie 100 km/h". Musimy wiedzieć, czy jedzie na północ, południe, wschód czy zachód to właśnie różnica między skalarną szybkością a wektorową prędkością. Wektory pozwalają nam precyzyjnie modelować rzeczywistość, gdzie wiele zjawisk ma konkretną orientację w przestrzeni.
Skalar vs. Wektor: Kluczowa różnica, którą musisz zrozumieć
Zrozumienie różnicy między skalarem a wektorem to jeden z pierwszych i najważniejszych kroków w fizyce. Skalary to wielkości, które są w pełni opisane przez jedną liczbę (wartość) i jednostkę. Przykładem może być masa, czas, temperatura czy energia. Kiedy mówię, że mam 5 kilogramów cukru, nie muszę dodawać, w którą stronę te kilogramy są skierowane to po prostu ilość. Wektory natomiast, jak już wspomniałem, wymagają podania czterech fundamentalnych cech: wartości (modułu), kierunku, zwrotu i punktu przyłożenia. Bez nich opis jest niekompletny i często bezsensowny. Na przykład, siła 10 N działająca w dół to zupełnie coś innego niż siła 10 N działająca w górę. Ta fundamentalna różnica sprawia, że wektory są niezastąpione w opisie dynamiki i kinematyki.
Przykłady z życia wzięte: Dlaczego siła i prędkość to wektory, a masa i czas to skalary?
Aby jeszcze lepiej zrozumieć tę kluczową różnicę, spójrzmy na kilka konkretnych przykładów z fizyki:
| Wielkości wektorowe | Wielkości skalarne |
|---|---|
| Siła: Posiada wartość (np. 10 N), kierunek (np. poziomy), zwrot (np. w prawo) i punkt przyłożenia. Bez tych informacji nie wiemy, jak obiekt zareaguje. | Masa: Opisuje ilość materii w obiekcie (np. 5 kg). Nie ma kierunku ani zwrotu. |
| Prędkość: Mówi o tym, jak szybko obiekt się porusza i w którą stronę (np. 60 km/h na północ). Jest kluczowa w opisie ruchu. | Czas: Mierzy interwał (np. 30 sekund). Nie ma kierunku. |
| Przyspieszenie: Opisuje zmianę wektora prędkości w czasie. Może zmienić wartość prędkości, jej kierunek, lub jedno i drugie. | Temperatura: Mierzy stopień nagrzania ciała (np. 25°C). Nie ma kierunku. |
| Przemieszczenie: Wskazuje na zmianę położenia obiektu od punktu początkowego do końcowego, z uwzględnieniem kierunku i zwrotu. | Energia: Zdolność do wykonania pracy (np. 100 J). Nie ma kierunku. |
| Pęd: Iloczyn masy i prędkości. Jest wektorem, ponieważ prędkość jest wektorem. | Droga: Całkowita długość ścieżki przebytej przez obiekt, bez względu na kierunek. |
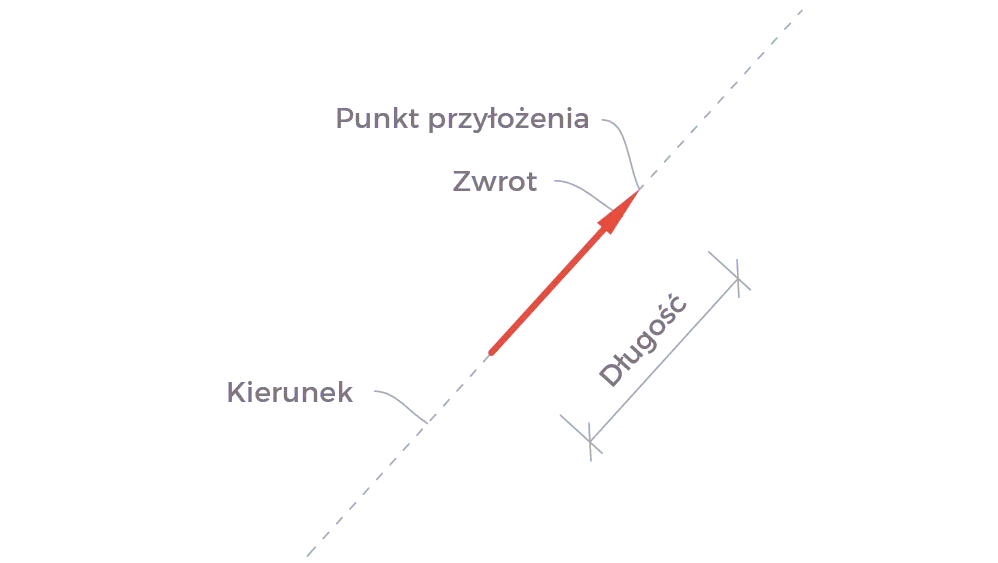
Anatomia wektora poznaj jego cztery fundamentalne cechy
Aby w pełni opisać wektor i zrozumieć jego działanie, musimy zawsze pamiętać o jego czterech fundamentalnych cechach. Każda z nich jest równie ważna i pominięcie którejkolwiek sprawi, że nasz opis będzie niekompletny lub błędny. Przyjrzyjmy się im bliżej.
Wartość (moduł): Jak "mocno" działa dana wielkość?
Wartość, zwana również modułem lub długością wektora, to dodatnia liczba wraz z jednostką, która określa "jak bardzo" lub "jak mocno" dana wielkość fizyczna działa. Na przykład, jeśli mówimy o sile, wartość będzie wyrażona w niutonach (np. 50 N). Graficznie, wartość wektora odpowiada po prostu długości strzałki, którą go reprezentujemy. Im dłuższa strzałka, tym większa wartość wektora.
Kierunek: Na jakiej linii "leży" wektor?
Kierunek wektora to prosta, wzdłuż której wektor działa. Może to być kierunek poziomy, pionowy, ukośny (np. pod kątem 30 stopni do poziomu). Ważne jest, aby pamiętać, że kierunek określa jedynie linię działania, a nie konkretną stronę. Na przykład, kierunek "pionowy" obejmuje zarówno ruch w górę, jak i w dół.
Zwrot: W którą stronę jest skierowany? Różnica między kierunkiem a zwrotem
Zwrot wektora wskazuje, w którą stronę na danym kierunku wektor jest skierowany. To właśnie grot strzałki symbolizuje zwrot. Aby to lepiej zrozumieć, pomyślmy o kierunku "pionowym". Na tym kierunku możemy mieć dwa przeciwne zwroty: w górę lub w dół. Podobnie na kierunku "poziomym" możemy mieć zwrot w prawo lub w lewo. Jest to kluczowa różnica: kierunek to linia, a zwrot to konkretna orientacja na tej linii. W fizyce często zdarza się, że dwie siły mają ten sam kierunek, ale przeciwne zwroty, co skutkuje ich wzajemnym znoszeniem się lub osłabianiem.
Punkt przyłożenia: Gdzie dokładnie zaczyna się działanie wektora?
Punkt przyłożeniato miejsce w przestrzeni, w którym wektor "zaczepia się" lub zaczyna działać. Jest to niezwykle ważne, szczególnie przy analizie sił. Siła działająca na środek ciężkości obiektu może wywołać ruch postępowy, podczas gdy ta sama siła przyłożona w innym punkcie może spowodować obrót obiektu. Wyobraźmy sobie pchanie drzwi pchnięcie blisko zawiasów będzie mniej efektywne niż pchnięcie daleko od nich, nawet jeśli wartość siły będzie taka sama. To właśnie punkt przyłożenia robi różnicę.
Jak przedstawić wektor wizualizacja i zapis matematyczny
Wektory są abstrakcyjnymi pojęciami, ale w fizyce i matematyce mamy ustalone sposoby ich reprezentacji, które ułatwiają zrozumienie i wykonywanie obliczeń. Zarówno graficzne, jak i symboliczne przedstawienie wektora jest niezwykle ważne.
Graficzna reprezentacja: Strzałka jako intuicyjny obraz wektora
Najbardziej intuicyjnym sposobem przedstawienia wektora jest użycie strzałki. Jak już wspomniałem, długość strzałki jest proporcjonalna do wartości (modułu) wektora. Linia, na której leży strzałka, określa kierunek wektora, a grot strzałki wskazuje jego zwrot. Punkt, z którego strzałka wychodzi, to punkt przyłożenia. Ta wizualizacja jest niezwykle pomocna, zwłaszcza na początku nauki, ponieważ pozwala szybko zorientować się w sytuacji i zrozumieć, jak różne wektory oddziałują ze sobą.
Zapis symboliczny: Jak poprawnie oznaczać wektory w zeszycie i podręczniku?
W zeszytach i podręcznikach wektory oznaczamy w specyficzny sposób, aby odróżnić je od skalarów. Najczęściej spotyka się dwie formy zapisu:
-
Pogrubiona litera: Na przykład,
F
oznacza wektor siły, av
wektor prędkości. -
Litera ze strzałką nad nią: Na przykład,
$\vec{F}$
lub$\vec{v}$
. Ten zapis jest często używany w ręcznych notatkach.
Wartość (moduł) wektora zapisujemy zazwyczaj jako zwykłą, niepogrubioną literę (np. F, v) lub jako wektor ujęty w pionowe kreski (np. |F| lub |$\vec{F}$|).
Wektory w układzie współrzędnych: Czym są składowe wektora?
Kiedy przenosimy wektory do świata analitycznego, czyli do układu współrzędnych (np. kartezjańskiego x, y dla dwóch wymiarów lub x, y, z dla trzech), możemy rozłożyć je na tak zwane składowe. Składowe to rzuty wektora na osie układu współrzędnych. Na przykład, wektor siły F w płaszczyźnie xy będzie miał składowe Fx i Fy. Taki zapis (np. F = [Fx, Fy]) umożliwia nam wykonywanie precyzyjnych obliczeń matematycznych, dodawanie, odejmowanie i inne operacje na wektorach, co jest podstawą rozwiązywania złożonych problemów fizycznych.
Najważniejsze wielkości wektorowe w fizyce gdzie je spotkasz?
Wektory są wszechobecne w fizyce. Bez nich niemożliwe byłoby precyzyjne opisanie wielu zjawisk, od prostego ruchu po skomplikowane pola. Oto kilka najważniejszych wielkości wektorowych, z którymi spotkasz się na każdym kroku.
Siła: Klucz do zrozumienia ruchu i równowagi
Siła jest prawdopodobnie najbardziej intuicyjnym przykładem wektora. Posiada wartość (jak mocno pchamy lub ciągniemy), kierunek (wzdłuż jakiej linii), zwrot (czy pchamy, czy ciągniemy) i punkt przyłożenia (gdzie dokładnie działamy). Zrozumienie siły jako wektora jest absolutnie kluczowe dla mechaniki. Bez tego nie da się analizować ruchu obiektów, równowagi statycznej czy dynamiki zderzeń. Przykłady sił to siła grawitacji, siła tarcia, siła sprężystości czy siła reakcji podłoża każda z nich ma swoją orientację w przestrzeni.
Prędkość i przyspieszenie: Matematyczny opis dynamiki ruchu
Kiedy mówimy o ruchu, prędkość i przyspieszenie są wektorami. Prędkość nie tylko informuje nas o tym, jak szybko obiekt się porusza (to jest skalarna szybkość), ale także w jakim kierunku i zwrocie. Samochód jadący 60 km/h na północ ma inną prędkość niż samochód jadący 60 km/h na wschód. Z kolei przyspieszenie opisuje, jak zmienia się wektor prędkości w czasie. Może ono zmieniać wartość prędkości (np. samochód przyspiesza na prostej), jej kierunek (np. samochód w zakręcie, nawet jeśli jego szybkość jest stała), albo jedno i drugie. To właśnie dzięki wektorowemu charakterowi przyspieszenia możemy opisywać ruch po okręgu czy ruch pocisku.
Przemieszczenie: Co innego niż droga, którą pokonałeś
Przemieszczenie to kolejna ważna wielkość wektorowa, którą często myli się ze skalarną drogą. Przemieszczenie jest wektorem, który łączy punkt początkowy ruchu z punktem końcowym. Jego wartość to najkrótsza odległość między tymi punktami, a kierunek i zwrot wskazują od punktu początkowego do końcowego. Droga natomiast to całkowita długość ścieżki, jaką przebył obiekt. Jeśli wyjdziesz z domu, pójdziesz do sklepu i wrócisz, twoje przemieszczenie wyniesie zero (punkt początkowy = punkt końcowy), ale droga będzie równa dwukrotnej odległości do sklepu. To pokazuje, jak ważne jest rozróżnienie tych pojęć.
Pęd, moment siły i natężenie pola: Inne kluczowe wektory w fizyce
Oprócz tych podstawowych, w fizyce spotykamy wiele innych ważnych wielkości wektorowych:
- Pęd: Jest to iloczyn masy obiektu (skalar) i jego prędkości (wektor). Pęd jest wektorem i odgrywa kluczową rolę w zasadzie zachowania pędu, np. w analizie zderzeń.
- Moment siły: Opisuje zdolność siły do wywoływania obrotu. Jest to wektor, którego kierunek jest prostopadły do płaszczyzny, w której działa siła i ramię siły.
- Natężenie pola (elektrycznego, magnetycznego, grawitacyjnego): Te wektory opisują siłę, jaka działa na jednostkowy ładunek (w polu elektrycznym), jednostkowy biegun magnetyczny (w polu magnetycznym) lub jednostkową masę (w polu grawitacyjnym) w danym punkcie przestrzeni. Ich kierunek i zwrot wskazują kierunek działania tej siły.
Podstawowe operacje jak "liczyć" na wektorach?
Wektory nie są tylko narzędziem do opisu; możemy na nich wykonywać podstawowe operacje matematyczne, które są niezbędne do rozwiązywania zadań i analizowania złożonych sytuacji fizycznych. Dodawanie, odejmowanie i mnożenie przez skalar to fundamenty, które musisz opanować.
Dodawanie wektorów: Jak znaleźć siłę wypadkową? (Metoda trójkąta i równoległoboku)
Dodawanie wektorów pozwala nam znaleźć tak zwany wektor wypadkowy, który reprezentuje sumaryczny efekt działania wielu wektorów. Istnieją dwie główne metody graficzne:
- Metoda trójkąta: Aby dodać dwa wektory, np. A i B, rysujemy pierwszy wektor A, a następnie z końca wektora A rysujemy początek wektora B. Wektor wypadkowy C = A + B to wektor łączący początek wektora A z końcem wektora B.
- Metoda równoległoboku: Jeśli dwa wektory A i B mają wspólny punkt przyłożenia, rysujemy je z tego samego punktu. Następnie dopełniamy rysunek do równoległoboku. Wektor wypadkowy C = A + B to przekątna tego równoległoboku, wychodząca ze wspólnego punktu przyłożenia.
Oprócz metod graficznych, wektory możemy dodawać również analitycznie, sumując ich odpowiednie składowe w układzie współrzędnych. Jeśli A = [Ax, Ay] i B = [Bx, By], to C = A + B = [Ax + Bx, Ay + By]. Ta metoda jest precyzyjniejsza i często wykorzystywana w obliczeniach.
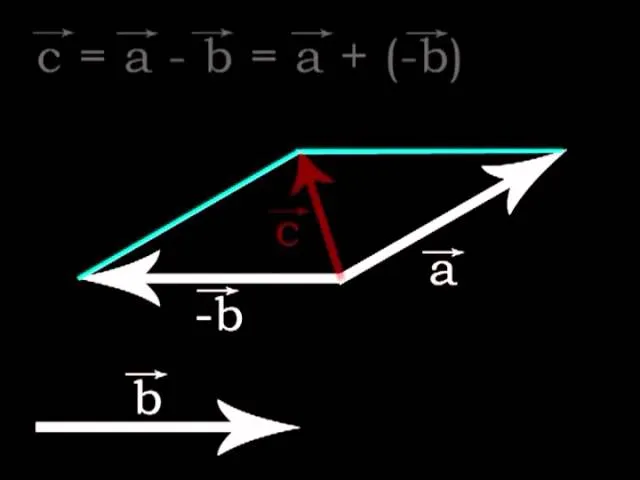
Odejmowanie wektorów: Co to jest wektor przeciwny?
Odejmowanie wektorów jest tak naprawdę szczególnym przypadkiem dodawania. Aby odjąć wektor B od wektora A (czyli obliczyć A - B), dodajemy do wektora A tak zwany wektor przeciwny do B. Wektor przeciwny do B (oznaczany jako -B) ma taką samą wartość i kierunek jak wektor B, ale przeciwny zwrot. Graficznie, po prostu odwracamy strzałkę wektora B i stosujemy metodę dodawania. Analitycznie, jeśli A = [Ax, Ay] i B = [Bx, By], to C = A - B = [Ax - Bx, Ay - By].
Mnożenie wektora przez skalar: Jak zmienić jego długość i zwrot?
Mnożenie wektora przez skalar (czyli przez zwykłą liczbę) jest prostą operacją, która wpływa na jego wartość i, ewentualnie, zwrot. Jeśli pomnożymy wektor A przez skalar k:
- Jeśli k jest dodatnie, wektor wynikowy (kA) będzie miał ten sam kierunek i zwrot co A, ale jego wartość zostanie pomnożona przez k. Na przykład, 2A będzie wektorem dwukrotnie dłuższym niż A.
- Jeśli k jest ujemne, wektor wynikowy (kA) będzie miał ten sam kierunek co A, ale jego wartość zostanie pomnożona przez |k|, a zwrot zmieni się na przeciwny. Na przykład, -1A to wektor przeciwny do A, a -2A to wektor dwukrotnie dłuższy niż A, ale o przeciwnym zwrocie.
Ta operacja jest często wykorzystywana do skalowania wektorów, np. do obliczania pędu (masa * prędkość) czy do zmiany jednostek.
Wektory w praktyce dlaczego ich zrozumienie jest niezbędne do rozwiązywania zadań?
Zrozumienie wektorów to nie tylko teoria to przede wszystkim potężne narzędzie do rozwiązywania praktycznych problemów fizycznych. Bez umiejętności pracy z wektorami, wiele zadań z mechaniki, dynamiki czy elektrodynamiki staje się niemożliwych do rozwiązania. Pokażę to na dwóch przykładach.
Rozkładanie sił na składowe: Analiza ruchu na równi pochyłej
Jednym z klasycznych zastosowań wektorów jest rozkładanie sił na składowe, co jest niezbędne do analizy ruchu na równi pochyłej. Wyobraź sobie klocek leżący na pochyłości. Działa na niego siła grawitacji (ciężkości), która jest skierowana pionowo w dół. Jednak aby zrozumieć, jak klocek będzie się poruszał, musimy rozłożyć tę siłę na dwie składowe: jedną równoległą do równi (odpowiedzialną za zsuwanie się) i drugą prostopadłą do równi (naciskającą na podłoże). Dzięki temu możemy obliczyć siłę tarcia, siłę normalną i ostatecznie przyspieszenie klocka. Bez wektorów i ich składowych, analiza takiego prostego zjawiska byłaby niezwykle skomplikowana.
Prędkość wypadkowa: Jak prąd rzeki wpływa na ruch łódki?
Inny świetny przykład to obliczanie prędkości wypadkowej. Wyobraź sobie łódkę, która próbuje przepłynąć rzekę. Łódka ma swoją prędkość względem wody, ale jednocześnie woda w rzece płynie z pewną prędkością względem brzegu. Aby obliczyć rzeczywistą prędkość łódki względem brzegu (prędkość wypadkową), musimy wektorowo dodać prędkość łódki i prędkość prądu rzeki. Jeśli łódka płynie prostopadle do brzegu, a prąd ją znosi, to jej rzeczywista trajektoria będzie ukośna. Tylko dzięki wektorowemu dodawaniu prędkości możemy precyzyjnie przewidzieć, gdzie łódka wyląduje na drugim brzegu. To pokazuje, jak wektory pozwalają nam łączyć różne ruchy i ich efekty w spójną całość.
Przeczytaj również: Niepewność pomiaru w fizyce: Co to? Obliczaj i zapisuj wyniki!
Podsumowanie: Kluczowe koncepcje, które warto zapamiętać
- Wektor to wielkość fizyczna, która oprócz wartości liczbowej posiada także kierunek i zwrot, co odróżnia ją od skalara.
- Do pełnego opisu wektora niezbędne są cztery cechy: wartość (moduł), kierunek, zwrot i punkt przyłożenia.
- Wektory są reprezentowane graficznie jako strzałki, a symbolicznie jako pogrubione litery lub litery ze strzałką nad nimi.
- Kluczowe wielkości wektorowe w fizyce to siła, prędkość, przyspieszenie, przemieszczenie, pęd i natężenie pól.
- Na wektorach można wykonywać operacje takie jak dodawanie, odejmowanie i mnożenie przez skalar, co jest podstawą rozwiązywania zadań fizycznych.