W świecie fizyki i wszelkich nauk eksperymentalnych, gdzie precyzja ma kluczowe znaczenie, pojęcie niepewności pomiaru jest absolutnie fundamentalne. To nie jest synonim "błędu" w potocznym rozumieniu, lecz raczej świadome i ilościowe określenie naszej niewiedzy, czy też wątpliwości co do prawdziwej wartości mierzonej wielkości. Zrozumienie, jak ją obliczać i poprawnie zapisywać, jest kluczowe dla każdego, kto chce rzetelnie analizować wyniki eksperymentalne i budować wiarygodną wiedzę.
Niepewność pomiaru to nie błąd klucz do rzetelnych wyników w fizyce
- Niepewność pomiaru to parametr charakteryzujący rozrzut wartości, które można przypisać mierzonej wielkości, a nie synonim błędu pomiarowego.
- Główne źródła niepewności to niedoskonałość przyrządów, błędy obserwatora, zmienne warunki otoczenia oraz niedoskonałość metody pomiarowej.
- Niepewności klasyfikuje się na typ A (wyznaczane statystycznie z serii pomiarów) i typ B (wyznaczane z informacji pozastatystycznych, np. specyfikacji przyrządu).
- Podstawowe miary to niepewność standardowa (u), złożona niepewność standardowa (uc) dla pomiarów pośrednich oraz niepewność rozszerzona (U), określająca przedział ufności.
- Ostateczny wynik pomiaru zawsze zapisuje się w formie x ± U, z odpowiednim zaokrągleniem wyniku i niepewności.
Czym tak naprawdę jest niepewność pomiaru i dlaczego to nie to samo co "błąd"?
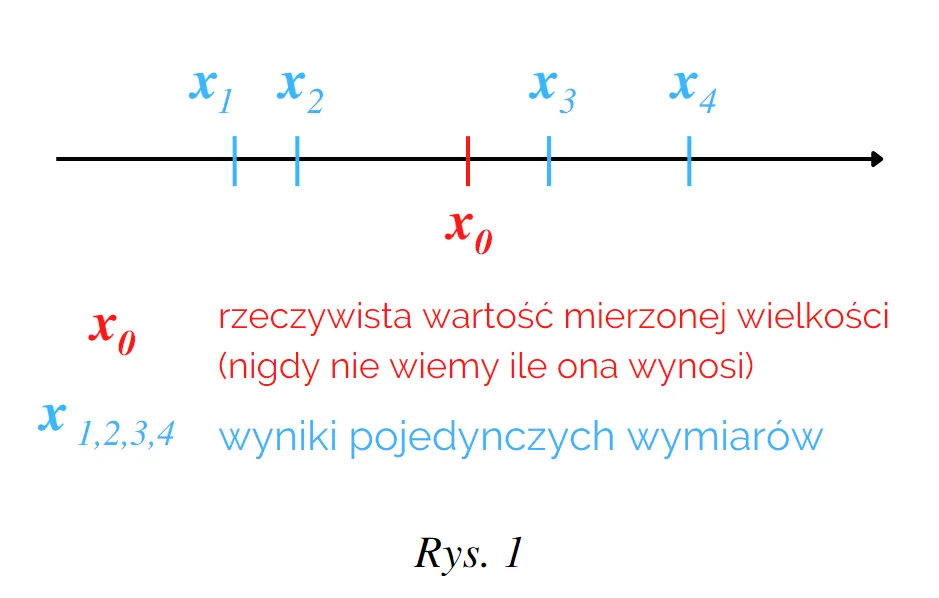
Kiedy mówimy o niepewności pomiaru w fizyce, często mylimy ją z potocznym rozumieniem "błędu". Tymczasem to dwa zupełnie różne pojęcia. Niepewność pomiaru to parametr charakteryzujący rozrzut wartości, które można w uzasadniony sposób przypisać mierzonej wielkości. To nasza kwantyfikacja wątpliwości co do tego, jak blisko wartość, którą uzyskaliśmy, jest wartości prawdziwej.
Błąd pomiarowy natomiast to różnica między wynikiem pomiaru a wartością prawdziwą mierzonej wielkości. Problem w tym, że wartość prawdziwa jest z natury rzeczy nieznana i często niemożliwa do dokładnego określenia. Dlatego też nie możemy obliczyć dokładnego błędu. Możemy jedynie próbować go minimalizować i oszacować, jak duża jest nasza niepewność co do wyniku.
Właśnie dlatego, jako fizycy i eksperymentatorzy, zawsze dążymy do tego, aby pełny, prawidłowy wynik pomiaru składał się z dwóch elementów: oszacowanej wartości wielkości mierzonej oraz podanej niepewności pomiaru. To klucz do transparentności i rzetelności.
Po co w ogóle zawracać sobie głowę niepewnością? Kluczowe znaczenie w nauce i technice
Można by zapytać, po co w ogóle zawracać sobie głowę tymi wszystkimi obliczeniami i analizami niepewności? Otóż, uwzględnianie niepewności jest absolutnie fundamentalne w nauce i technice, a ja osobiście uważam, że to jeden z filarów rzetelnej pracy eksperymentalnej. Pozwala nam na wiarygodną analizę wyników eksperymentalnych, umożliwia porównywanie danych uzyskanych z różnych źródeł, przez różnych badaczy, a także ocenę, czy nasze wyniki są zgodne z przewidywaniami teoretycznymi. Bez niepewności, każdy pomiar byłby jedynie pojedynczą liczbą, której wiarygodność byłaby niemożliwa do oceny, a to w nauce jest po prostu niedopuszczalne.
Skąd biorą się niepewności? Poznaj najczęstsze źródła niedokładności pomiarów
Przyrząd pomiarowy jako pierwsze ogniwo: klasa dokładności, rozdzielczość i wzorcowanie
Nawet najlepszy przyrząd pomiarowy nie jest idealny i zawsze wprowadza pewne ograniczenia, które stają się źródłem niepewności. Mówimy tu o jego ograniczonej dokładności, która często jest określona przez producenta jako klasa przyrządu. Kolejnym czynnikiem jest rozdzielczość, czyli najmniejsza zmiana mierzonej wielkości, jaką przyrząd jest w stanie zarejestrować. Wreszcie, każdy przyrząd wymaga regularnego wzorcowania, aby upewnić się, że jego wskazania są zgodne z międzynarodowymi wzorcami. Niewzorcowany lub źle wzorcowany przyrząd jest pewnym źródłem dodatkowych niepewności.
Rola obserwatora: błąd paralaksy, czas reakcji i inne czynniki ludzkie
Człowiek, jako obserwator i operator, jest nieodłącznym elementem wielu procesów pomiarowych, a co za tym idzie, również źródłem niepewności. Klasycznym przykładem jest błąd paralaksy, który pojawia się przy odczytywaniu wskazań z analogowych skal, gdy linia wzroku nie jest prostopadła do skali. Innym czynnikiem jest czas reakcji, szczególnie istotny w pomiarach dynamicznych, gdzie precyzyjne uruchomienie lub zatrzymanie stopera zależy od refleksu eksperymentatora. Moje doświadczenie pokazuje, że nawet najbardziej doświadczeni badacze muszą być świadomi tych ograniczeń.
Wpływ otoczenia: jak temperatura, wilgotność czy drgania wpływają na wynik?
Warunki zewnętrzne, w których przeprowadzamy pomiary, często są zmienne i mogą znacząco wpływać na wyniki, generując niepewności. Na przykład, temperatura może wpływać na rozszerzalność materiałów, zmieniając długość liniałów czy objętość cieczy. Ciśnienie atmosferyczne ma znaczenie w pomiarach gęstości gazów, a wilgotność może wpływać na właściwości elektryczne materiałów. Nawet subtelne drgania w laboratorium mogą zakłócać precyzyjne pomiary, na przykład w optyce czy mikroskopii. Dlatego tak ważne jest kontrolowanie i monitorowanie środowiska pomiarowego.
Niedoskonałość samej metody: uproszczenia i założenia w procedurze pomiarowej
Często zapominamy, że sama metoda pomiarowa, którą stosujemy, również może być źródłem niepewności. Żadna metoda nie jest idealna; każda opiera się na pewnych uproszczeniach i założeniach, które mogą odbiegać od rzeczywistości. Na przykład, zakładamy, że obiekt ma idealnie regularny kształt, co w praktyce rzadko ma miejsce. Czasem problemem jest również niedoskonała definicja wielkości mierzonej czy na pewno wiemy, co dokładnie mierzymy i czy nasza metoda faktycznie to odzwierciedla? To są subtelności, które mogą mieć duży wpływ na końcową niepewność.
Klasyfikacja niepewności: metody typu A i B
Niepewność typu A: siła statystyki w serii powtarzalnych pomiarów
W fizyce i metrologii stosujemy dwie główne metody wyznaczania niepewności. Niepewność typu A to taka, którą wyznaczamy metodami statystycznymi na podstawie serii powtarzalnych pomiarów. Kiedy wykonujemy wiele pomiarów tej samej wielkości, wyniki zazwyczaj nieco się różnią. Niepewność typu A, dla serii n pomiarów, jest równa odchyleniu standardowemu średniej arytmetycznej. Jest to miara rozrzutu przypadkowych wyników, czyli tego, jak bardzo poszczególne pomiary różnią się od ich średniej wartości. Im więcej pomiarów wykonamy, tym precyzyjniej możemy oszacować tę niepewność.
Niepewność typu B: gdy statystyka nie wystarcza rola wiedzy o przyrządzie i warunkach
Nie zawsze mamy możliwość wykonania serii pomiarów, a nawet jeśli ją mamy, statystyka nie obejmuje wszystkich źródeł niepewności. Wtedy z pomocą przychodzi niepewność typu B, którą wyznaczamy na podstawie informacji pozastatystycznych. Źródłem tych informacji może być dokumentacja techniczna przyrządu (np. klasa dokładności, rozdzielczość), dane literaturowe, świadectwa wzorcowania, a nawet moje własne doświadczenie i zdrowy rozsądek eksperymentatora. To jest ten rodzaj niepewności, który wymaga głębokiej znajomości używanego sprzętu i warunków eksperymentu.
Porównanie metod: kiedy stosować typ A, kiedy typ B, a kiedy obie naraz?
W praktyce rzadko kiedy stosujemy tylko jeden typ niepewności. Niepewność typu A jest dominująca, gdy mamy do czynienia z losowymi fluktuacjami wyników, na przykład przy pomiarach czasu, gdzie czas reakcji operatora jest znaczący. Niepewność typu B jest kluczowa, gdy ograniczenia wynikają z samego przyrządu, np. jego rozdzielczości. Często jednak musimy łączyć oba typy niepewności. Dla pomiarów bezpośrednich, całkowitą niepewność standardową (u(x)) obliczamy jako pierwiastek z sumy kwadratów niepewności typu A i B: u(x) = √(uA² + uB²). To podejście pozwala nam uwzględnić wszystkie istotne źródła niepewności.
Obliczanie niepewności pomiaru: od teorii do praktyki
Scenariusz 1: Obliczanie niepewności dla serii pomiarów (metoda typu A)
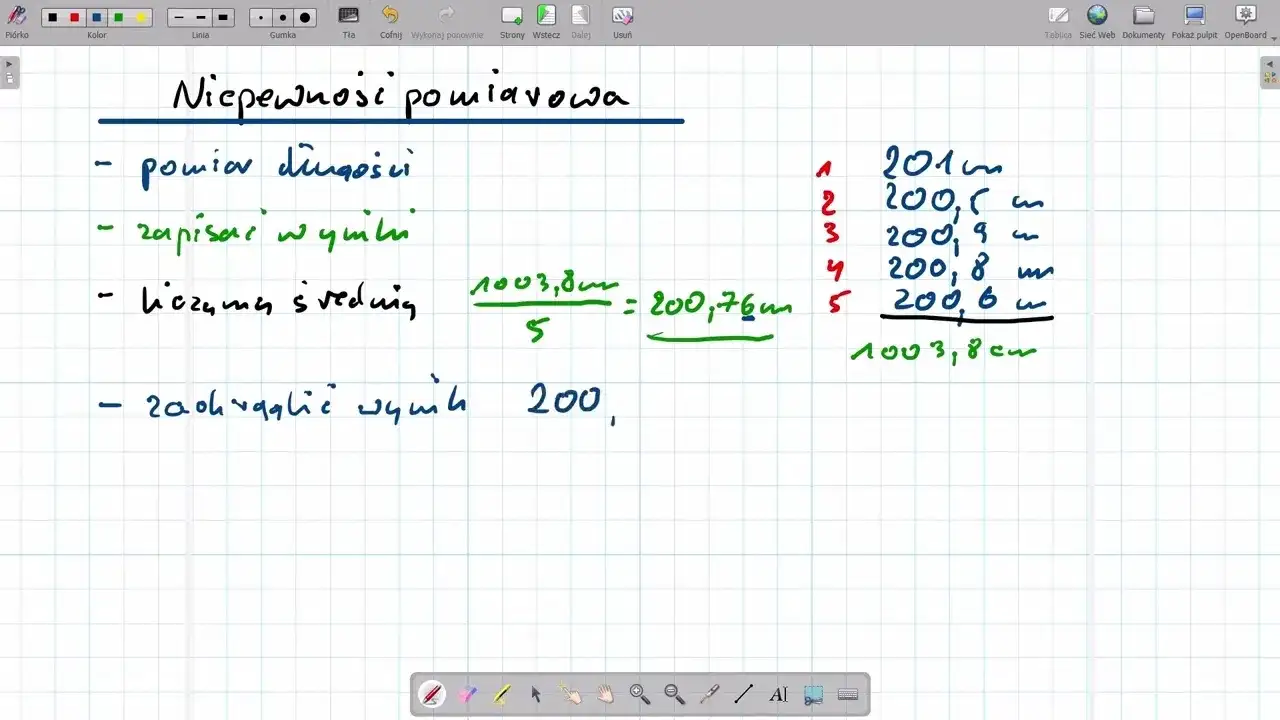
Kiedy wykonujemy serię pomiarów tej samej wielkości, nasza najlepsza strategia to wykorzystanie statystyki. Pozwala nam to na oszacowanie niepewności typu A, która jest miarą losowego rozrzutu wyników. Przejdźmy przez kroki, które sam stosuję w laboratorium.
Krok 1: Obliczanie średniej arytmetycznej jako najlepszego przybliżenia wartości
Dla serii pomiarów x₁, x₂, ..., xₙ, najlepszym estymatorem wartości mierzonej wielkości jest średnia arytmetyczna. To intuicyjne uśredniając wiele wyników, "wygładzamy" przypadkowe fluktuacje. Wzór na średnią arytmetyczną jest prosty:
x̅ = (x₁ + x₂ + ... + xₙ) / n
Krok 2: Wyznaczanie odchylenia standardowego średniej klucz do niepewności
Niepewność standardową typu A (uA) obliczamy, korzystając ze wzoru na odchylenie standardowe średniej arytmetycznej. Ten parametr mówi nam, jak bardzo średnia z naszych pomiarów może różnić się od prawdziwej wartości. Ogólny wzór na odchylenie standardowe średniej to:
uA = s / √n
gdzie 's' to odchylenie standardowe pojedynczego pomiaru, a 'n' to liczba pomiarów. Odchylenie standardowe 's' obliczamy ze wzoru:
s = √[ Σ(xᵢ - x̅)² / (n - 1) ]
Scenariusz 2: Szacowanie niepewności dla pojedynczego pomiaru (metoda typu B)
Co jednak, gdy nie możemy wykonać serii pomiarów, a mamy tylko jeden wynik? Wtedy musimy polegać na metodzie typu B, czyli na naszej wiedzy o przyrządzie i warunkach pomiaru. To wymaga nieco więcej doświadczenia i intuicji.
Analiza przyrządów analogowych: reguła "połowy działki elementarnej"
Dla przyrządów analogowych, takich jak linijki, suwmiarki czy woltomierze ze wskazówką, często stosujemy regułę "połowy najmniejszej działki elementarnej". Jeśli najmniejsza działka na skali wynosi np. 1 mm, to przyjmujemy, że nasza niepewność typu B wynosi 0,5 mm. Wynika to z założenia, że jesteśmy w stanie odczytać wartość z dokładnością do połowy tej najmniejszej podziałki.
Analiza przyrządów cyfrowych: jak interpretować specyfikację producenta?
W przypadku przyrządów cyfrowych, takich jak multimetry czy wagi elektroniczne, kluczowa jest specyfikacja producenta. Zazwyczaj podaje on klasę dokładności (np. ±0,5% odczytu + 2 cyfry) lub rozdzielczość (np. 0,01 V). Niepewność typu B szacujemy, biorąc pod uwagę te dane. Jeśli na przykład miernik cyfrowy ma rozdzielczość 0,01 V, to często przyjmujemy niepewność równą połowie tej rozdzielczości, czyli 0,005 V, lub opieramy się na bardziej szczegółowych danych z instrukcji.
Łączenie niepewności: jak obliczyć całkowitą niepewność standardową (uA i uB)?
Gdy mamy już oszacowane niepewności typu A i typu B dla pomiaru bezpośredniego, musimy je połączyć, aby uzyskać całkowitą niepewność standardową u(x). Robimy to, dodając kwadraty tych niepewności i biorąc z tego pierwiastek. To tak zwana zasada sumowania kwadratowego, która zakłada, że niepewności te są niezależne. Wzór wygląda następująco:
u(x) = √(uA² + uB²)
Dzięki temu uzyskujemy jedną, spójną miarę niepewności, która uwzględnia zarówno losowe fluktuacje, jak i ograniczenia sprzętowe czy metodyczne.
Prawo propagacji niepewności: pomiary pośrednie
Czym jest pomiar pośredni i dlaczego wymaga specjalnego podejścia?
Wiele wielkości fizycznych nie da się zmierzyć bezpośrednio. Zamiast tego, wyznaczamy je na podstawie pomiarów innych, bardziej podstawowych wielkości. Taki rodzaj pomiaru nazywamy pomiarem pośrednim. Na przykład, aby obliczyć gęstość obiektu, musimy zmierzyć jego masę i objętość. Ponieważ każda z tych mierzonych wielkości (masa, objętość) obarczona jest własną niepewnością, musimy mieć sposób na to, aby te niepewności "przenieść" na wynik końcowy. To właśnie dlatego pomiary pośrednie wymagają specjalnego podejścia do obliczania niepewności.
Złożona niepewność standardowa: jak przenieść niepewności z pomiarów prostych na wynik końcowy?
Do przenoszenia niepewności z pomiarów prostych na wynik końcowy służy nam prawo propagacji niepewności, które pozwala obliczyć złożoną niepewność standardową (uc(x)). Idea jest taka, że jeśli wielkość końcowa jest funkcją kilku innych wielkości, to jej niepewność zależy od niepewności tych składowych i od tego, jak "czuła" jest funkcja na zmiany każdej z nich. W praktyce często wykorzystuje się do tego pochodne cząstkowe funkcji, ale najważniejsze jest zrozumienie, że niepewności składowe nie sumują się w prosty sposób, lecz są "propagowane" przez wzór, który łączy te wielkości.
Praktyczne przykłady: obliczanie niepewności dla pola powierzchni, gęstości lub prędkości
Aby lepiej zrozumieć prawo propagacji niepewności, spójrzmy na kilka uproszczonych przykładów:
- Pole powierzchni prostokąta: Jeśli mierzymy długość (a ± u(a)) i szerokość (b ± u(b)) prostokąta, to pole P = a * b. Niepewność pola u(P) będzie zależała od u(a) i u(b) w sposób, który odzwierciedla ich względny wpływ na wynik.
- Gęstość obiektu: Gęstość ρ = m / V, gdzie m to masa (m ± u(m)), a V to objętość (V ± u(V)). Złożona niepewność gęstości uc(ρ) będzie wynikać z niepewności masy i objętości.
- Prędkość: Prędkość v = s / t, gdzie s to przebyta droga (s ± u(s)), a t to czas (t ± u(t)). Niepewność prędkości uc(v) będzie zależała od niepewności pomiaru drogi i czasu.
W każdym z tych przypadków, prawo propagacji niepewności dostarcza nam narzędzi do obliczenia, jak niepewności poszczególnych pomiarów wpływają na niepewność ostatecznego, pośrednio wyznaczonego wyniku.
Finalny szlif: poprawny zapis wyniku i niepewność rozszerzona
Niepewność rozszerzona (U): czym jest współczynnik rozszerzenia (k) i jak określa poziom ufności?
Po obliczeniu złożonej niepewności standardowej (uc(x)), musimy ją przekształcić w niepewność rozszerzoną (U). Jest to miara, która określa przedział wokół wyniku pomiaru, w którym z określonym prawdopodobieństwem (poziomem ufności) znajduje się wartość rzeczywista. Aby to zrobić, mnożymy uc(x) przez współczynnik rozszerzenia (k). Najczęściej, dla większości zastosowań, przyjmuje się k=2. Ten współczynnik odpowiada poziomowi ufności około 95%, co oznacza, że z 95% pewnością możemy stwierdzić, że prawdziwa wartość mierzonej wielkości leży w przedziale określonym przez wynik ± U. To bardzo praktyczne podejście, które daje nam konkretną informację o wiarygodności naszego pomiaru.
Złote zasady zapisu: prawidłowe zaokrąglanie i formatowanie ostatecznego wyniku (x ± U)
Poprawny zapis wyniku pomiaru jest równie ważny jak samo jego obliczenie. To wizytówka naszej pracy. Oto "złote zasady", których zawsze przestrzegam:
- Ogólna forma zapisu: Ostateczny wynik pomiaru zawsze zapisujemy w postaci: x ± U, wraz z podaniem jednostki. Na przykład: (10,25 ± 0,03) cm.
- Zaokrąglanie niepewności: Niepewność rozszerzoną (U) zazwyczaj zaokrąglamy do jednej lub dwóch cyfr znaczących. Jeśli pierwsza cyfra znacząca niepewności jest 1 lub 2, często zaokrąglam do dwóch cyfr znaczących, aby zachować większą precyzję. W innych przypadkach jedna cyfra znacząca jest wystarczająca.
- Zaokrąglanie wyniku: Wynik pomiaru (x) musi być zaokrąglony do tej samej liczby miejsc po przecinku co niepewność rozszerzona (U). To kluczowa zasada, która zapewnia spójność i czytelność. Jeśli niepewność ma dwie cyfry po przecinku, wynik też musi mieć dwie.
Przeczytaj również: Pogoda pod lupą: Od termometru po satelitę co mierzy atmosferę?
Interpretacja wyniku: co tak naprawdę mówi nam przedział ufności?
Kiedy już mamy zapisany wynik w formie x ± U, co to tak naprawdę oznacza? Ten przedział ufności mówi nam, że jeśli powtórzylibyśmy nasz pomiar wiele razy, to w około 95% przypadków (dla k=2) prawdziwa wartość mierzonej wielkości znalazłaby się w tym właśnie przedziale. To nie jest deklaracja, że prawdziwa wartość jest dokładnie taka, jaką zmierzyliśmy, ale raczej określenie zakresu, w którym z dużą pewnością możemy się jej spodziewać. To właśnie ta informacja sprawia, że nasze wyniki są wiarygodne i użyteczne w dalszych analizach naukowych i technicznych.