Elipsa w fizyce: Jak prawa Keplera kształtują kosmiczne orbity?

Ten artykuł szczegółowo wyjaśni, czym jest elipsa, jakie są jej kluczowe parametry i dlaczego jest ona tak fundamentalna dla zrozumienia zjawisk fizycznych, zwłaszcza w astronomii. Dowiesz się, jak elipsy opisują ruch planet i jak siła grawitacji kształtuje kosmiczne orbity.

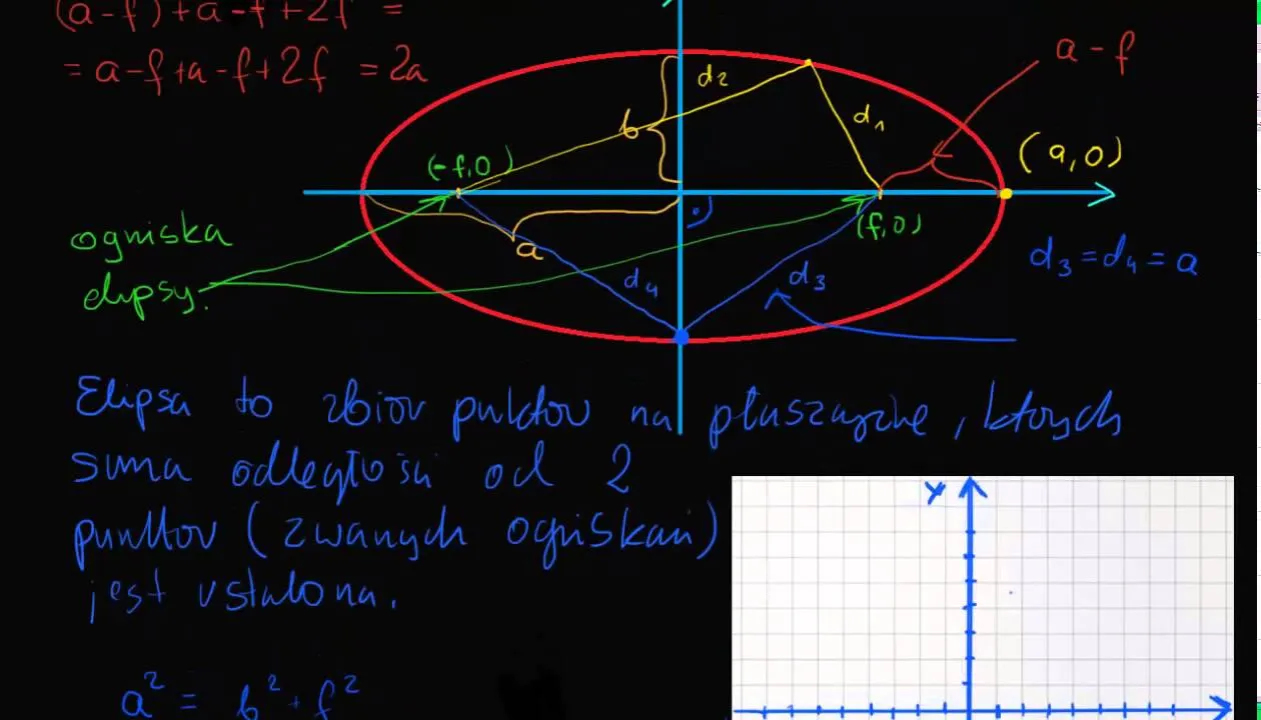
Czym jest elipsa? Intuicyjna definicja wykraczająca poza matematykę

Elipsa to fascynująca krzywa stożkowa, którą możemy sobie wyobrazić jako zbiór wszystkich punktów na płaszczyźnie, dla których suma odległości od dwóch stałych punktów, zwanych ogniskami, jest zawsze taka sama. To właśnie ta stała suma odległości nadaje elipsie jej charakterystyczny, spłaszczony kształt koła. W przeciwieństwie do okręgu, który ma jedno centrum, elipsa ma dwa "centra" te właśnie ogniska. To prosta, a zarazem potężna definicja, która pozwala nam zrozumieć jej naturę bez zagłębiania się w skomplikowane równania.

Od geometrii do fizyki: Gdzie w praktyce spotykamy elipsy?

Choć elipsa wydaje się być pojęciem czysto geometrycznym, jej znaczenie w fizyce jest absolutnie fundamentalne. Najważniejszym i najbardziej spektakularnym przykładem jest oczywiście astronomia. Elipsy opisują orbity planet, komet, asteroid i innych ciał niebieskich krążących wokół gwiazd. To właśnie dzięki elipsie rozumiemy, jak poruszają się planety w naszym Układzie Słonecznym i dlaczego ich odległość od Słońca nie jest stała. Ale, jak się przekonamy, zastosowania elipsy wykraczają daleko poza kosmos, znajdując swoje miejsce nawet w medycynie czy architekturze.

Anatomia elipsy kluczowe pojęcia

Aby w pełni zrozumieć rolę elipsy w fizyce, musimy najpierw poznać jej podstawowe elementy. To one decydują o kształcie i rozmiarze tej krzywej, a w konsekwencji na przykład o charakterystyce kosmicznej orbity.

Ogniska: Tajemnicze punkty, które definiują wszystko

Jak już wspomniałem, ogniska (F1, F2) to dwa stałe punkty wewnątrz elipsy, które są absolutnie kluczowe dla jej definicji. To od nich mierzymy sumę odległości do dowolnego punktu na elipsie. Ich położenie ma bezpośredni wpływ na kształt elipsy: im bliżej siebie leżą ogniska, tym bardziej elipsa przypomina okrąg. Jeśli ogniska się pokrywają, elipsa staje się idealnym okręgiem. Im dalej są od siebie, tym bardziej elipsa jest "spłaszczona".

Półoś wielka i mała: Jak mierzyć i opisywać elipsę?

Elipsa ma dwie główne osie symetrii. Oś wielka (2a) to najdłuższa średnica elipsy, która przechodzi przez oba ogniska i jej środek. Z kolei oś mała (2b) to najkrótsza średnica, prostopadła do osi wielkiej i również przechodząca przez środek elipsy. W fizyce częściej posługujemy się pojęciami półosi wielkiej (a) i półosi małej (b), które są po prostu połowami długości tych osi. Półoś wielka (a) jest szczególnie ważna w astronomii, ponieważ często reprezentuje średnią odległość planety od Słońca.

Mimośród (ekscentryczność): Od idealnego koła do spłaszczonej orbity

Mimośród, często oznaczany literą e, to miara "spłaszczenia" elipsy. Definiujemy go jako stosunek odległości między ogniskiem a środkiem elipsy (oznaczanej jako c) do długości półosi wielkiej (a), czyli e = c/a. Wartość mimośrodu dla elipsy zawsze mieści się w przedziale od 0 do 1. Kiedy e = 0, ogniska pokrywają się ze środkiem, a elipsa staje się idealnym okręgiem. Im bliżej e jest wartości 1, tym bardziej elipsa jest spłaszczona. Na przykład, orbita Ziemi ma bardzo mały mimośród (około 0,0167), co oznacza, że jest prawie okręgiem. Orbity komet mogą mieć znacznie większe mimośrody, co sprawia, że są bardzo wydłużone.

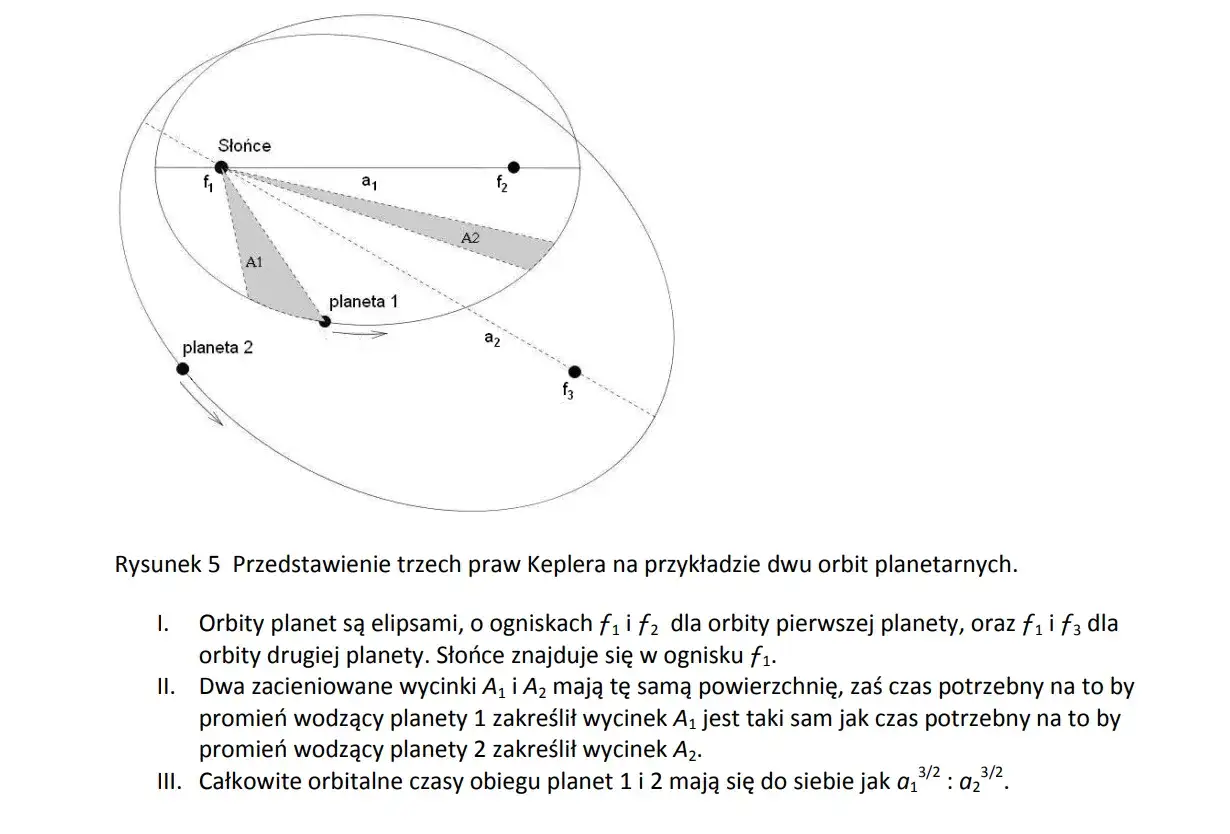
Prawa Keplera jak elipsy rządzą ruchem planet

Zrozumienie anatomii elipsy jest kluczowe do pojęcia praw, które zrewolucjonizowały astronomię. Johannes Kepler, na początku XVII wieku, sformułował trzy prawa, które precyzyjnie opisują ruch planet wokół Słońca, umieszczając elipsę w samym sercu kosmicznej mechaniki.

Pierwsze Prawo Keplera: Słońce nie leży w centrum!

Pierwsze Prawo Keplera głosi, że każda planeta Układu Słonecznego porusza się po orbicie w kształcie elipsy, a Słońce znajduje się w jednym z jej ognisk. To była rewolucyjna myśl! Wcześniej sądzono, że orbity są idealnymi okręgami, a Słońce leży w ich centrum. Odkrycie Keplera oznaczało, że odległość planety od Słońca nie jest stała, lecz zmienia się w ciągu roku, co ma istotne konsekwencje dla klimatu i pór roku.

Drugie Prawo Keplera: Dlaczego planety zwalniają i przyspieszają?

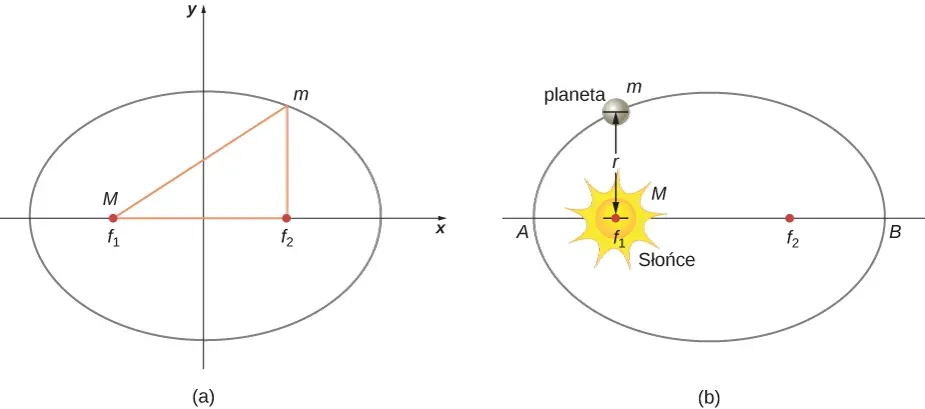
Drugie Prawo Keplera, zwane również prawem pól, mówi, że promień wodzący planety (linia łącząca Słońce z planetą) zakreśla w równych odstępach czasu równe pola powierzchni. Co to oznacza w praktyce? Jeśli planeta jest bliżej Słońca, musi poruszać się szybciej, aby w tym samym czasie zakreślić tę samą powierzchnię co wtedy, gdy jest dalej od Słońca. To wyjaśnia, dlaczego planety przyspieszają w pobliżu Słońca i zwalniają, gdy są od niego oddalone. Jest to bezpośrednia konsekwencja zasady zachowania momentu pędu fundamentalnej zasady fizyki.

Peryhelium i aphelium: Kiedy jesteśmy najbliżej, a kiedy najdalej od Słońca?

Zgodnie z Pierwszym Prawem Keplera, odległość planety od Słońca zmienia się. Punkt na orbicie eliptycznej, w którym planeta jest najbliżej Słońca, nazywamy peryhelium. Z kolei punkt, w którym planeta znajduje się najdalej od Słońca, to aphelium. Dla Ziemi peryhelium przypada na początek stycznia, a aphelium na początek lipca, co pokazuje, że nasza odległość od Słońca ma mniejszy wpływ na pory roku niż nachylenie osi obrotu Ziemi.

Trzecie Prawo Keplera: Kosmiczna harmonia łącząca odległość i czas

Trzecie Prawo Keplera, znane jako prawo harmonii, stwierdza, że stosunek kwadratu okresu obiegu planety (T²) do sześcianu wielkiej półosi jej orbity (a³) jest stały dla wszystkich planet w Układzie Słonecznym. Matematycznie wyrażamy to jako T²/a³ = const. To prawo jest niezwykle ważne, ponieważ pozwala nam porównywać orbity różnych planet i przewidywać ich okresy obiegu, jeśli znamy ich półosie wielkie, lub odwrotnie. Pokazuje ono, że istnieje głęboka, matematyczna harmonia w ruchach ciał niebieskich.

Siła grawitacji Newtona ostateczne wyjaśnienie eliptycznych orbit

Prawa Keplera były empirycznymi odkryciami, opartymi na skrupulatnych obserwacjach. Prawdziwe zrozumienie, *dlaczego* planety poruszają się po elipsach, przyszło wraz z Izaakiem Newtonem i jego prawem powszechnego ciążenia.

Jak grawitacja "zmusza" planety do poruszania się po elipsie?

Isaac Newton, bazując na pracach Keplera i Galileusza, sformułował prawo powszechnego ciążenia, które mówi, że każde dwa ciała przyciągają się wzajemnie siłą proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu odległości między ich środkami. Newton udowodnił matematycznie, że ruch ciała pod wpływem takiej siły centralnej, odwrotnie proporcjonalnej do kwadratu odległości, musi prowadzić do torów w kształcie krzywych stożkowych czyli elips, parabol lub hiperbol. To było triumfalne połączenie teorii z obserwacją, które ostatecznie wyjaśniło eliptyczne orbity planet. Siła grawitacji "zakrzywia" tor ruchu planety w taki sposób, że pozostaje ona w zamkniętej orbicie eliptycznej wokół Słońca.

Elipsa, parabola, hiperbola: Kiedy orbita staje się drogą w jedną stronę?

W kontekście siły grawitacji, elipsa jest tylko jednym z możliwych kształtów orbity. Rozróżniamy trzy typy krzywych stożkowych, które mogą opisywać ruch ciała w polu grawitacyjnym:

• Elipsa: Jest to orbita zamknięta, charakteryzująca się ujemną energią całkowitą. Ciało jest "uwięzione" w polu grawitacyjnym i będzie krążyć wokół centralnego obiektu w nieskończoność (lub do momentu zderzenia/zmiany orbity). Większość planet i asteroid ma orbity eliptyczne.
• Parabola: Jest to orbita otwarta, gdy ciało ma energię całkowitą równą zero. Oznacza to, że ciało przelatuje obok centralnego obiektu tylko raz i ucieka z jego pola grawitacyjnego, nigdy nie wracając. Niektóre komety mogą poruszać się po orbitach parabolicznych.
• Hiperbola: Również orbita otwarta, ale z dodatnią energią całkowitą. Ciało ma jeszcze większą prędkość niż w przypadku paraboli i również ucieka z pola grawitacyjnego, przelatując obok centralnego obiektu tylko raz. Jest to typowa orbita dla obiektów, które wlatują w układ gwiezdny z zewnątrz i mają wystarczającą prędkość, by go opuścić.

Wszystkie te tory są konsekwencją prawa powszechnego ciążenia Newtona i początkowych warunków ruchu ciała.

Nie tylko kosmos zaskakujące zastosowania elipsy na Ziemi

Choć elipsa jest nierozerwalnie związana z astronomią, jej unikalne właściwości geometryczne znajdują praktyczne zastosowania również tutaj, na Ziemi, w wielu dziedzinach fizyki i inżynierii.

Optyczne i akustyczne właściwości: fenomen "galerii szeptów"

Jedną z najbardziej fascynujących właściwości elipsy jest jej zdolność do skupiania fal. Promień (czy to światła, czy dźwięku) wychodzący z jednego ogniska elipsy, po odbiciu od jej wewnętrznej powierzchni, zawsze przechodzi przez drugie ognisko. To zjawisko jest wykorzystywane w tzw. "galeriach szeptów", które można znaleźć w niektórych katedrach czy budynkach publicznych. Stojąc w jednym ognisku i szepcząc, osoba w drugim ognisku, nawet oddalona o wiele metrów, może usłyszeć szept z niezwykłą klarownością, podczas gdy osoby stojące pomiędzy ogniskami nic nie słyszą. To pokazuje, jak precyzyjnie elipsa potrafi skupiać energię falową.

Jak elipsa pomaga w medycynie i technice?

Wspomniana właściwość skupiania fal znajduje również zastosowanie w medycynie, zwłaszcza w procedurze zwanej litotrypsją. Jest to nieinwazyjna metoda kruszenia kamieni nerkowych za pomocą fal uderzeniowych. W urządzeniu do litotrypsji generator fal uderzeniowych umieszcza się w jednym ognisku eliptycznego reflektora. Kamień nerkowy pacjenta jest precyzyjnie pozycjonowany w drugim ognisku. Fale uderzeniowe, odbijając się od reflektora, skupiają się dokładnie na kamieniu, krusząc go bez uszkadzania otaczających tkanek. To doskonały przykład, jak abstrakcyjne pojęcie geometryczne może ratować życie i poprawiać zdrowie.

Elipsa w języku fizyki równanie i jego interpretacja

Dla fizyka i inżyniera, elipsa to nie tylko kształt, ale także matematyczny opis. Równanie elipsy pozwala na precyzyjne modelowanie i analizowanie jej właściwości w różnych kontekstach.

Zrozumienie wzoru (x²/a²) + (y²/b²) = 1

W kartezjańskim układzie współrzędnych, najprostsza forma równania elipsy, której środek znajduje się w punkcie (0,0), wygląda następująco: (x²/a²) + (y²/b²) = 1. W tym równaniu:

• x i y to współrzędne dowolnego punktu leżącego na elipsie.
• a to długość półosi wielkiej.
• b to długość półosi małej.

To równanie jest fundamentalne, ponieważ pozwala nam opisać każdy punkt na elipsie, znając jedynie jej rozmiary. Jest to podstawa do dalszych obliczeń i analiz w mechanice, optyce czy inżynierii.

Przeczytaj również: Fizyka kwantowa: Przewodnik po świecie, który zmienia rzeczywistość

Jak parametry elipsy wpływają na jej równanie?

Zmiana wartości a (półosi wielkiej) i b (półosi małej) w równaniu elipsy bezpośrednio wpływa na jej kształt i rozmiar.

• Jeśli a = b, równanie upraszcza się do x² + y² = a², co jest równaniem okręgu. Potwierdza to, że okrąg jest szczególnym przypadkiem elipsy.
• Jeśli a > b, elipsa jest spłaszczona wzdłuż osi X (poziomo).
• Jeśli b > a, elipsa jest spłaszczona wzdłuż osi Y (pionowo).

Im większa różnica między a i b, tym bardziej elipsa jest wydłużona lub spłaszczona. To proste równanie pozwala nam modelować szeroki zakres eliptycznych kształtów, od niemal idealnych okręgów po bardzo wydłużone orbity komet, co jest niezmiernie cenne w fizyce i astronomii.