W fizyce, aby zrozumieć, jak cokolwiek się porusza, musimy najpierw odpowiedzieć na fundamentalne pytanie: jaką drogę przebywa ten obiekt w przestrzeni? To właśnie tutaj wkracza pojęcie toru ruchu kluczowe dla całej kinematyki, czyli działu fizyki zajmującego się opisem ruchu. Jako Daniel Kowalski, wiem, że to pojęcie bywa mylone z innymi, podobnymi, dlatego w tym artykule postaram się w prosty i przystępny sposób wyjaśnić, czym jest tor ruchu, jakie są jego rodzaje i dlaczego jego zrozumienie jest tak ważne. Obiecuję, że unikniemy skomplikowanych wzorów, skupiając się na intuicyjnym pojęciu.
Tor ruchu w fizyce esencja drogi, jaką pokonuje obiekt
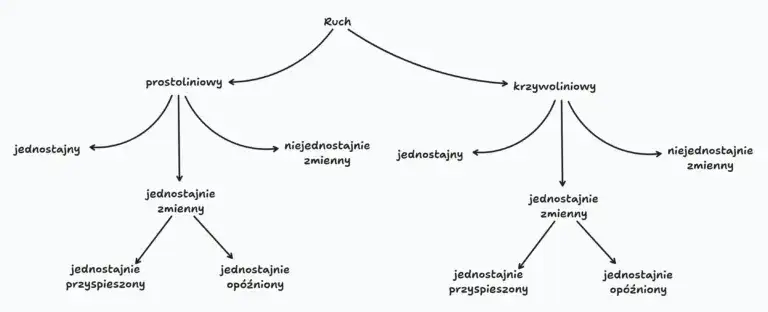
- Tor ruchu to linia zakreślana w przestrzeni przez poruszające się ciało lub punkt materialny.
- Może być linią prostą (ruch prostoliniowy) lub krzywą (ruch krzywoliniowy), w zależności od charakteru ruchu.
- Różni się od "drogi" (długości toru) i "przemieszczenia" (wektora łączącego punkt początkowy z końcowym).
- Kształt toru jest determinowany przez siły działające na obiekt.
- Pojęcie "punktu materialnego" jest uproszczeniem, które pomaga fizykom analizować ruch.
- Opis toru zawsze zależy od wybranego układu odniesienia.
Definicja, która rozjaśni wszystko: Co to jest tor?
Zacznijmy od sedna. W fizyce tor ruchu, nazywany również trajektorią, to nic innego jak linia, którą zakreśla w przestrzeni poruszające się ciało lub, w uproszczeniu, punkt materialny. Wyobraź sobie ślad, jaki zostawia samolot na niebie, smugę dymu za rakietą, czy nawet niewidzialną ścieżkę, którą podąża rzucona piłka to wszystko są tory ruchu. Ta linia może być prosta lub krzywa, a jej kształt mówi nam bardzo wiele o samym ruchu.
Dlaczego linia ma tak duże znaczenie w opisie ruchu?
Może się wydawać, że to tylko linia, ale w fizyce ma ona kolosalne znaczenie. Wizualizacja ruchu jako linii jest fundamentalna, ponieważ pozwala nam na graficzne przedstawienie całej ścieżki, którą obiekt pokonuje. Dzięki temu możemy analizować, gdzie obiekt był, gdzie jest teraz i gdzie będzie w przyszłości. To podstawa kinematyki działu fizyki, który zajmuje się opisem ruchu bez wnikania w jego przyczyny. Bez zrozumienia toru ruchu, trudno byłoby nam mówić o prędkości, przyspieszeniu czy nawet o tym, jak siły wpływają na ruch obiektu.
Punkt materialny: jak fizycy upraszczają świat, by go zrozumieć?
W definicji toru ruchu wspomniałem o "punkcie materialnym". To bardzo ważne uproszczenie, które fizycy stosują, aby ułatwić sobie życie i analizę. Punkt materialny to wyidealizowany model ciała fizycznego, w którym jego rozmiary i kształt są pomijane, a cała masa jest skupiona w jednym punkcie. Kiedy analizujemy ruch Ziemi wokół Słońca, nie interesuje nas, czy Ziemia jest kulą, czy ma góry i doliny dla celów obliczeniowych traktujemy ją jako punkt. Podobnie, rzucając kamieniem, często pomijamy jego kształt i rozmiar, skupiając się na ruchu jego środka masy. To uproszczenie jest niezwykle przydatne, gdy rozmiary obiektu są dużo mniejsze niż odległości, które pokonuje, lub gdy nie interesuje nas ruch obrotowy ciała.
Prosta czy krzywa? Odkryj dwa podstawowe rodzaje torów ruchu
Kiedy już wiemy, czym jest tor ruchu, możemy przejść do jego klasyfikacji. W zależności od kształtu, tory ruchu dzielimy na dwa główne rodzaje, które w dużej mierze determinują, jak opiszemy dany ruch.
Ruch prostoliniowy: Kiedy świat porusza się jak po sznurku
Zacznijmy od najprostszego przypadku. Ruch prostoliniowy to taki, w którym tor ruchu jest idealną linią prostą. To oznacza, że obiekt porusza się zawsze w tym samym kierunku, bez żadnych zakrętów czy odchyleń. Przykładów nie brakuje: pociąg jadący po prostym odcinku torów, samochód poruszający się autostradą bez skręcania, czy też spadające swobodnie jabłko (jeśli pominiemy opory powietrza) wszystkie te obiekty poruszają się po torze prostoliniowym. W takim ruchu analiza jest zazwyczaj najłatwiejsza, ponieważ nie musimy martwić się o zmiany kierunku.
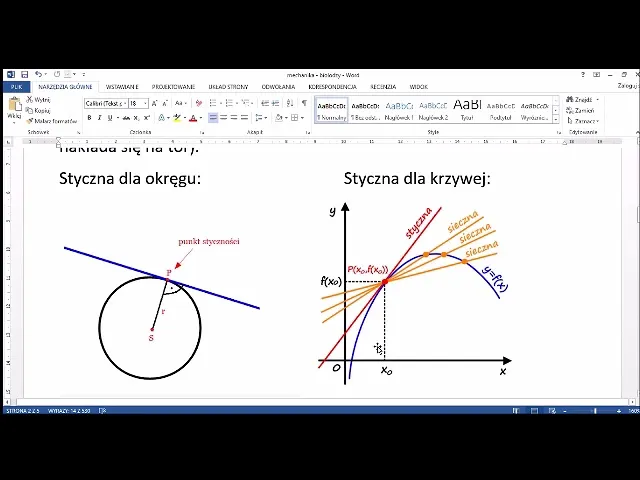
Ruch krzywoliniowy: Prawdziwe oblicze ruchu w otaczającym nas świecie
Choć ruch prostoliniowy jest prosty do zrozumienia, to ruch krzywoliniowy jest zdecydowanie najczęstszym rodzajem ruchu, jaki obserwujemy w otaczającym nas świecie. Tutaj tor ruchu jest linią krzywą może to być łuk, okrąg, elipsa, parabola, a nawet bardzo skomplikowana, nieregularna krzywa. Piłka kopnięta przez piłkarza, planeta krążąca wokół Słońca, czy samochód pokonujący zakręt wszystkie te obiekty poruszają się po torach krzywoliniowych. To właśnie w ruchu krzywoliniowym dzieje się najwięcej i tu fizyka pokazuje swoje najbardziej fascynujące oblicze.
Tor, droga, przemieszczenie: poznaj różnice i unikaj popularnych błędów
To jest moment, w którym często dochodzi do nieporozumień. Tor ruchu, droga i przemieszczenie to pojęcia ze sobą powiązane, ale bynajmniej nie tożsame. Zrozumienie ich różnic jest kluczowe dla każdego, kto chce opanować podstawy fizyki.
Tor ruchu, czyli "mapa" podróży obiektu
Jak już wiemy, tor ruchu to kształt, "mapa" ścieżki, którą obiekt pokonuje. To geometryczny zbiór wszystkich punktów, przez które przeszedł obiekt podczas swojego ruchu. Tor sam w sobie nie mówi nam, jak szybko obiekt się poruszał, ani ile czasu mu to zajęło mówi nam jedynie, którędy.
Droga: jak długa była ta "mapa"?
Gdy mamy już tor ruchu, możemy zmierzyć jego długość. I właśnie to jest droga (oznaczana literą s) całkowita długość toru ruchu, czyli odległość, jaką faktycznie pokonało ciało. Droga jest wielkością skalarną, co oznacza, że ma tylko wartość (np. 10 metrów), ale nie ma kierunku ani zwrotu. Co ważne, droga zawsze jest wartością nieujemną. Niezależnie od tego, jak bardzo się kręcisz w miejscu, twoja droga rośnie.
Przemieszczenie: liczy się tylko start i meta
I tu pojawia się największa różnica. Przemieszczenie (oznaczane jako Δr) to wektor, który łączy położenie początkowe obiektu z jego położeniem końcowym. Wektor oznacza, że przemieszczenie ma zarówno wartość (długość), jak i kierunek oraz zwrot. Wyobraź sobie prostą linię, strzałkę, która wskazuje, dokąd obiekt się przeniósł, niezależnie od tego, jaką skomplikowaną ścieżkę pokonał po drodze. Wartość przemieszczenia jest równa drodze tylko w bardzo specyficznym przypadku: w ruchu prostoliniowym, bez zmiany zwrotu.
Praktyczny przykład: Dlaczego po jednym okrążeniu stadionu Twoje przemieszczenie wynosi zero?
Aby to wszystko lepiej zrozumieć, posłużmy się klasycznym przykładem. Wyobraź sobie, że biegasz po owalnym stadionie. Startujesz z punktu A, robisz pełne okrążenie i wracasz do punktu A. Co się dzieje z Twoim torem, drogą i przemieszczeniem?
- Tor ruchu: To owalna linia bieżni, którą przebiegłeś.
- Droga: Przebiegłeś całą długość bieżni, powiedzmy 400 metrów. Twoja droga wynosi 400 m.
- Przemieszczenie: Skoro wróciłeś do punktu, z którego wystartowałeś, Twoje położenie początkowe i końcowe są identyczne. Oznacza to, że Twoje przemieszczenie wynosi zero! Mimo że pokonałeś dużą drogę, nie przemieściłeś się względem punktu startu.
Ten przykład doskonale pokazuje, jak ważne jest rozróżnianie tych trzech pojęć. Tor to kształt, droga to jego długość, a przemieszczenie to prosta linia od startu do mety.
Jak wyglądają tory ruchu w praktyce? Niesamowite przykłady z życia i nauki
Teraz, gdy znamy już podstawy, przyjrzyjmy się kilku najbardziej charakterystycznym i fascynującym torom ruchu, które spotykamy zarówno w codziennym życiu, jak i w zaawansowanej fizyce.
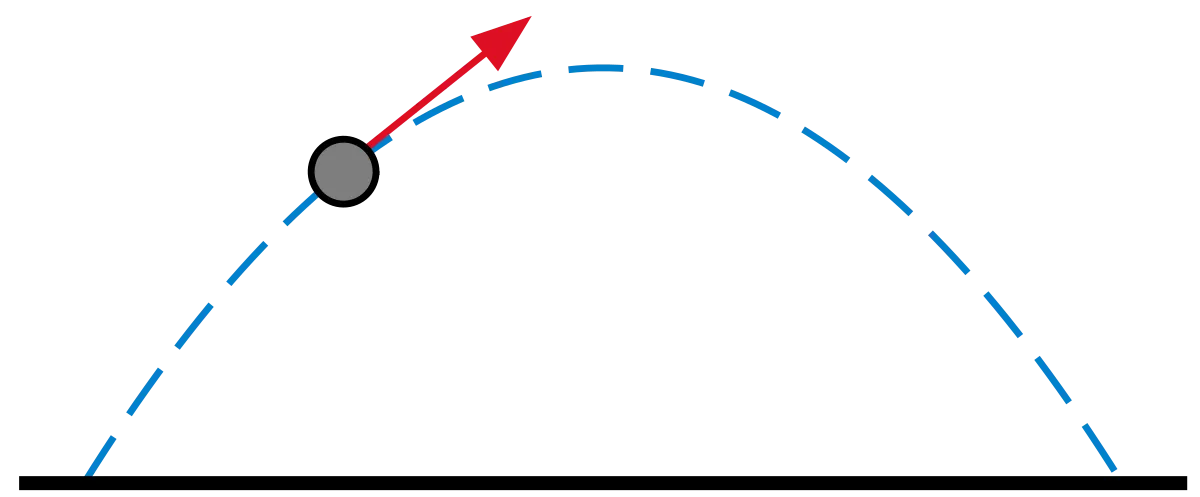
Parabola: Tor rzuconej piłki i fontanny wody
Jednym z najczęściej spotykanych torów krzywoliniowych jest parabola. Widzimy ją wszędzie tam, gdzie obiekt porusza się pod wpływem grawitacji, a opory powietrza są pomijalne. Kiedy rzucisz kamień ukośnie w górę, jego tor będzie miał kształt paraboli. Podobnie piłka kopnięta przez piłkarza, woda tryskająca z fontanny, czy nawet pocisk wystrzelony z działa (w przybliżeniu, bez uwzględnienia oporów powietrza) wszystkie te obiekty podążają paraboliczną ścieżką. To dlatego, że grawitacja nieustannie "ciągnie" je w dół, zakrzywiając ich początkowy ruch.
Elipsa: Jak planety, w tym Ziemia, tańczą wokół Słońca
Przenieśmy się w kosmos. Elipsa to tor, który jest doskonale znany astronomom. To właśnie po eliptycznych orbitach planety, w tym nasza Ziemia, krążą wokół Słońca. Również księżyce krążą wokół planet po torach eliptycznych. Odkrycie, że ruch planet odbywa się po elipsach, było jednym z kamieni milowych w rozwoju nauki i pozwoliło na precyzyjne przewidywanie ich położenia.
Okrąg: Dlaczego czujesz siłę na karuzeli?
Okrąg to kolejny bardzo ważny tor ruchu. Znamy go z karuzeli, gdzie ruch punktu na jej obwodzie jest idealnie okrągły. Podobnie, punkt na obwodzie obracającego się koła samochodu, czy satelita na orbicie geostacjonarnej wszystkie te obiekty poruszają się po okręgu. Kiedy jedziesz na karuzeli, czujesz, jak coś "ciągnie" Cię na zewnątrz to siła bezwładności, która jest efektem działania siły dośrodkowej, utrzymującej Cię na torze kołowym. Bez tej siły, po prostu odleciałbyś w linii prostej.
Od chaosu do porządku: Od ruchów Browna po linie śrubowe
Świat fizyki oferuje nam jeszcze bardziej złożone i fascynujące tory. Na przykład, ruchy Browna to chaotyczne, łamane tory, po których poruszają się mikroskopijne cząstki zawieszone w płynie, zderzając się z cząsteczkami otoczenia. To przykład toru, który jest nieregularny i nieprzewidywalny w krótkim okresie. Z drugiej strony, mamy piękną i uporządkowaną linię śrubową, po której porusza się naładowana cząstka w jednorodnym polu magnetycznym. To pokazuje, jak ogromna jest różnorodność torów ruchu i jak wiele zjawisk fizycznych można za ich pomocą opisać.
Co kształtuje tor ruchu? Rola sił w zakrzywianiu trajektorii
Zastanawiałeś się kiedyś, dlaczego obiekty poruszają się po takich, a nie innych torach? Odpowiedź leży w siłach, które na nie działają. To siły są architektami torów ruchu.
Dlaczego bez siły ruch odbywa się po linii prostej?
Klucz do zrozumieniatego leży w pierwszej zasadzie dynamiki Newtona, znanej jako zasada bezwładności. Mówi ona, że w inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła zewnętrzna lub działające siły równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Innymi słowy, jeśli nic nie przeszkadza obiektowi, będzie on poruszał się po idealnie prostej linii ze stałą prędkością. To jest jego "naturalny" stan ruchu. Siła jest potrzebna, aby ten stan zmienić aby obiekt przyspieszył, zwolnił lub, co najważniejsze dla naszego tematu, zmienił kierunek ruchu, czyli zakrzywił swój tor.
Jak siła grawitacji zakrzywia tor rzuconego kamienia?
Najlepszym przykładem, jak siła zakrzywia tor, jest wspomniany już rzut kamieniem. Kiedy rzucasz kamień, nadajesz mu pewną prędkość początkową. Gdyby nie było grawitacji, kamień leciałby prosto w nieskończoność. Ale ponieważ działa na niego siła grawitacji, która nieustannie ciągnie go w dół, tor kamienia staje się krzywoliniowy paraboliczny. Grawitacja jest siłą niezrównoważoną, której kierunek nie jest styczny do początkowego toru, co powoduje ciągłą zmianę kierunku wektora prędkości, a tym samym zakrzywienie toru.
Układ odniesienia ma znaczenie: Jak ten sam ruch może wyglądać inaczej?
Na koniec warto wspomnieć o czymś, co często jest pomijane: układ odniesienia. To ciało lub układ ciał, względem którego opisujemy ruch. Opis ruchu jest zawsze względny i zależy od tego, jaki układ odniesienia wybierzemy. Pomyśl o pasażerze siedzącym w pędzącym pociągu. Względem pociągu, pasażer jest w spoczynku (jego tor to punkt). Ale dla obserwatora stojącego na peronie, ten sam pasażer porusza się po linii prostej, z prędkością pociągu. To ten sam ruch, ale jego opis i kształt toru są różne w zależności od punktu widzenia. To pokazuje, jak ważne jest zawsze określenie, względem czego opisujemy ruch.
Czy tor ruchu można opisać matematycznie? Krótkie spojrzenie na równanie toru
Mimo że obiecałem unikać skomplikowanych wzorów, warto wspomnieć, że fizycy potrafią opisać tor ruchu w bardzo precyzyjny sposób za pomocą matematyki.
Od zależności czasowych do kształtu: Jak powstaje równanie toru?
W kinematyce ruch ciała opisuje się zazwyczaj za pomocą równań, które określają jego położenie (np. współrzędne x i y) w funkcji czasu: x(t) i y(t). Te równania mówią nam, gdzie obiekt znajduje się w każdej chwili. Ale co, jeśli chcemy poznać sam kształt toru, niezależnie od czasu? Wtedy możemy wyeliminować parametr czasu (t) z tych równań. W rezultacie otrzymujemy jedno równanie, które opisuje zależność jednej współrzędnej od drugiej (np. y(x)). To właśnie jest równanie toru ruchu, które matematycznie przedstawia jego kształt czy to parabola, elipsa, czy prosta.
Przeczytaj również: Pogoda pod lupą: Od termometru po satelitę co mierzy atmosferę?
Dlaczego matematyczny opis toru jest tak ważny w technologii i inżynierii?
Matematyczny opis toru ruchu ma ogromne znaczenie praktyczne. W inżynierii pozwala na precyzyjne projektowanie maszyn i urządzeń, od robotów przemysłowych po systemy nawigacyjne. W balistyce umożliwia dokładne przewidywanie, gdzie spadnie pocisk. W astronomii pozwala na obliczanie orbit satelitów i planet. W robotyce jest kluczowy do programowania ruchów ramion robotów. Bez tej precyzji, którą daje matematyka, wiele dziedzin technologii i nauki po prostu by nie istniało. To pokazuje, że choć pojęcie toru ruchu może wydawać się proste, jego konsekwencje i zastosowania są dalekosiężne.