Cześć! Jeśli fizyka sprawia Ci trudności, a zamiana jednostek przyprawia o ból głowy, to doskonale rozumiem Twoje frustracje. Wiem z doświadczenia, że to jedno z tych zagadnień, które na początku wydaje się skomplikowane, ale w rzeczywistości opiera się na kilku prostych zasadach. Ten poradnik został stworzony właśnie po to, by krok po kroku przeprowadzić Cię przez proces przeliczania jednostek, pokazując, że to umiejętność, którą każdy może opanować.
Zamiana jednostek w fizyce: proste metody na opanowanie trudnych zadań
- Zrozumienie systemu SI i przedrostków: Międzynarodowy Układ Jednostek Miar (SI) to podstawa. Kluczowe przedrostki to kilo (10³), centy (10⁻²), mili (10⁻³) oraz mega (10⁶). Ich znajomość to Twój punkt wyjścia do sprawnych przeliczeń.
- Zastosowanie metody "łańcuszkowej" (analiza wymiarowa): To najbezpieczniejsza technika. Polega na mnożeniu wartości przez "jedynkę" w postaci ułamka (np. 1 km / 1000 m), co pozwala na skracanie niechcianych jednostek i uzyskanie pożądanego wyniku.
- Kluczowe przeliczniki dla długości, masy i prędkości: Pamiętaj, że 1 m = 100 cm = 1000 mm, a 1 km = 1000 m. Dla masy: 1 kg = 100 dag = 1000 g, 1 t = 1000 kg. Prędkość to często problem: 1 m/s = 3,6 km/h. Aby zamienić km/h na m/s, dzielimy przez 3,6, a m/s na km/h mnożymy przez 3,6.
- Specyfika przeliczania jednostek pola i objętości: To tu najczęściej pojawiają się błędy! Pamiętaj, że przelicznik liniowy musisz podnieść do odpowiedniej potęgi. Np. 1 m² to nie 100 cm², lecz 10 000 cm² (bo 1 m = 100 cm, więc 1 m² = (100 cm)²). Podobnie dla objętości: 1 m³ = 1 000 000 cm³. Pamiętaj też, że 1 litr = 1 dm³ = 1000 cm³.
- Najczęstsze błędy i sposoby ich unikania: Uważaj na mylenie mnożenia z dzieleniem, ignorowanie potęg przy jednostkach pola i objętości oraz na chaotyczny zapis obliczeń. Metoda łańcuszkowa i uporządkowany zapis to Twoi najlepsi sprzymierzeńcy.
Zrozumienie problemu: To nie magia, to czysta logika
Zapewne nie raz zastanawiałeś się, dlaczego zamiana jednostek wydaje się tak trudna. Czy to jakaś tajemna wiedza, dostępna tylko dla nielicznych? Nic bardziej mylnego! W rzeczywistości, przeliczanie jednostek w fizyce opiera się na bardzo prostych i logicznych zasadach. Kluczem do zrozumienia jest pojęcie "jedynki" czyli mnożenie przez ułamek, w którym licznik i mianownik są sobie równe, ale wyrażone w różnych jednostkach. To właśnie ta "magiczna jedynka" pozwala nam płynnie przechodzić między różnymi skalami, nie zmieniając wartości fizycznej, a jedynie jej przedstawienie.
Klucz do sukcesu: Jedna prosta zasada, która zmienia wszystko
Pozwól, że rozwinę tę koncepcję "jedynki". Wyobraź sobie, że wiesz, iż 1 kilometr to to samo co 1000 metrów. Możesz to zapisać jako ułamek: 1 km / 1000 m lub 1000 m / 1 km. Oba te ułamki mają wartość 1! Gdy pomnożysz jakąkolwiek liczbę przez 1, jej wartość się nie zmieni, prawda? I tu tkwi cała tajemnica. Wybierając odpowiedni ułamek jednostkowy, możesz "skrócić" jednostki, których nie chcesz, i wprowadzić te, które są Ci potrzebne. To uniwersalna i niezwykle skuteczna zasada, którą zaraz pokażę Ci w praktyce.
Jak ten poradnik krok po kroku rozwiąże Twój problem z jednostkami?
Wierzę, że po przeczytaniu tego artykułu Twoje podejście do zamiany jednostek całkowicie się zmieni. Nauczysz się:
- Poznawać i rozumieć Międzynarodowy Układ Jednostek Miar (SI) oraz jego kluczowe przedrostki, które są fundamentem wszelkich przeliczeń.
- Opanować metodę łańcuszkową, która jest uniwersalnym i niezawodnym narzędziem do przeliczania dowolnych jednostek, nawet tych najbardziej złożonych.
- Zrozumieć i bezbłędnie stosować przeliczniki dla najczęściej spotykanych wielkości, takich jak długość, masa, prędkość, pole powierzchni i objętość.
- Rozpoznawać i unikać typowych błędów, które często prowadzą do pomyłek, a także dowiesz się, jak uporządkowany zapis może Ci w tym pomóc.
System SI i przedrostki: Twoi sojusznicy w fizyce
Czym jest Układ SI i dlaczego ułatwia życie każdemu fizykowi?
Międzynarodowy Układ Jednostek Miar, czyli w skrócie SI (od francuskiego Système International d'Unités), to nic innego jak uniwersalny język, którym posługują się naukowcy na całym świecie. Pomyśl o nim jak o wspólnym standardzie, który sprawia, że niezależnie od tego, czy jesteś w Polsce, Japonii czy Stanach Zjednoczonych, 1 metr zawsze będzie oznaczał tę samą długość, a 1 kilogram tę samą masę. To właśnie dzięki SI możemy bez problemu porównywać wyniki eksperymentów, wymieniać się danymi i wspólnie rozwijać naukę. Bez niego panowałby chaos, a obliczenia byłyby koszmarem!
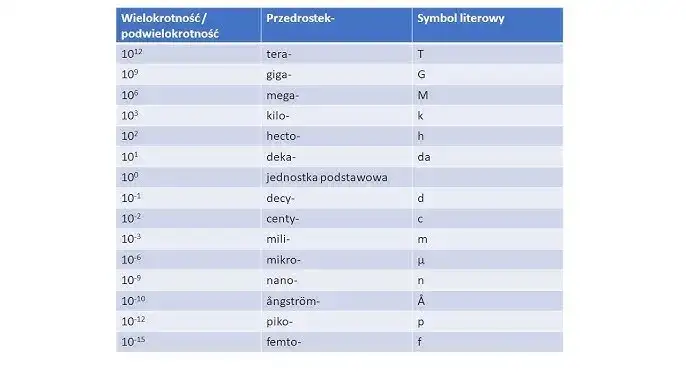
Twoja tajna broń: Tabela przedrostków, którą musisz znać
Przedrostki SI to małe dodatki do jednostek, które pozwalają nam wyrażać bardzo duże lub bardzo małe wartości w sposób zwięzły i zrozumiały. Zamiast pisać "1000 metrów", mówimy "1 kilometr". Zamiast "0,001 metra", mówimy "1 milimetr". To ogromne ułatwienie! Poniżej przedstawiam tabelę z najważniejszymi przedrostkami, które warto znać. Zwróć szczególną uwagę na te, które pogrubiłem to one najczęściej pojawiają się w szkolnej fizyce.
| Przedrostek (Symbol) | Wartość (Mnożnik) |
|---|---|
| deka (da) | 10¹ |
| hekto (h) | 10² |
| kilo (k) | 10³ |
| mega (M) | 10⁶ |
| giga (G) | 10⁹ |
| tera (T) | 10¹² |
| decy (d) | 10⁻¹ |
| centy (c) | 10⁻² |
| mili (m) | 10⁻³ |
| mikro (µ) | 10⁻⁶ |
| nano (n) | 10⁻⁹ |
| piko (p) | 10⁻¹² |
Przedrostki na co dzień: Kilo, centy, mili gdzie je spotykasz?
Przedrostki SI są tak powszechne, że używamy ich na co dzień, często nie zdając sobie z tego sprawy. Gdy kupujesz kilogram ziemniaków, używasz przedrostka "kilo", oznaczającego 1000 gramów. Mierząc coś linijką, często posługujesz się centymetrami (1/100 metra) lub milimetrami (1/1/1000 metra). W aptece możesz spotkać się z mililitrami leku. Nawet pojemność dysku twardego komputera wyrażana jest w gigabajtach (Giga = 10⁹) czy terabajtach (Tera = 10¹²). Widzisz, to wcale nie jest abstrakcyjna wiedza, tylko część naszej codzienności!
Metoda łańcuszkowa: Bezpieczna droga do prawidłowych przeliczeń
Jak działa "magiczny" ułamek, który zawsze daje dobry wynik?
Metoda łańcuszkowa, znana również jako analiza wymiarowa, to moim zdaniem najbardziej niezawodny sposób na zamianę jednostek. Jej "magia" polega na tym, że zamiast zastanawiać się, czy pomnożyć, czy podzielić, po prostu mnożymy przez odpowiednio skonstruowane ułamki, które mają wartość 1. Przykładowo, wiemy, że 1 kilometr to 1000 metrów. Możemy więc zapisać ułamek jednostkowy jako (1 km / 1000 m) lub (1000 m / 1 km). Oba te ułamki są równe 1. Kiedy chcesz przeliczyć jednostkę, wybierasz taki ułamek, aby niechciana jednostka znalazła się w mianowniku i mogła się skrócić z jednostką wyjściową. To jak układanie klocków jednostki, których nie potrzebujesz, po prostu znikają, a zostają te, które chcesz uzyskać.
Krok po kroku: Przeliczamy kilometry na centymetry bez ryzyka błędu
Przyjrzyjmy się, jak to działa w praktyce. Załóżmy, że chcemy przeliczyć 2,5 kilometra na centymetry. To zadanie, które często sprawia problemy, ale z metodą łańcuszkową jest proste:
-
Zapisz wartość, którą chcesz przeliczyć:
2,5 km
-
Zidentyfikuj jednostki pośrednie i ich przeliczniki:
Wiemy, że 1 km = 1000 m i 1 m = 100 cm.
-
Stwórz ułamki jednostkowe:
Z przelicznika 1 km = 1000 m tworzymy ułamek (1000 m / 1 km). Z przelicznika 1 m = 100 cm tworzymy ułamek (100 cm / 1 m).
-
Pomnóż wartość początkową przez ułamki jednostkowe, tak aby jednostki się skracały:
2,5 km * (1000 m / 1 km) * (100 cm / 1 m)
-
Skróć jednostki:
Jednostka "km" skraca się z "km" w mianowniku pierwszego ułamka. Jednostka "m" skraca się z "m" w mianowniku drugiego ułamka.
-
Wykonaj obliczenia:
2,5 * 1000 * 100 cm = 250 000 cm
Jak widzisz, wynik to 250 000 cm. Dzięki temu, że jednostki się skracają, zawsze wiesz, że idziesz w dobrym kierunku i trudniej o pomyłkę.
Przykład z życia wzięty: Ile metrów ma rolka papieru o długości 0, 025 km?
Wyobraź sobie, że masz rolkę papieru o długości 0,025 km i chcesz wiedzieć, ile to metrów. Stosujemy naszą metodę łańcuszkową. Zaczynamy od wartości początkowej i mnożymy przez ułamek jednostkowy, który pozwoli nam skrócić kilometry i uzyskać metry:
0,025 km * (1000 m / 1 km) = 25 m
Jednostka "km" skraca się, zostawiając nam "m". Rolka papieru ma więc 25 metrów długości. Proste, prawda?
Długość i masa: Podstawy przeliczania jednostek
Metr, kilometr, centymetr: Jak płynnie poruszać się po skali długości?
Długość to jedna z najczęściej mierzonych wielkości. Oto podstawowe jednostki i ich wzajemne relacje, które musisz znać:
- 1 metr (m) = 100 centymetrów (cm)
- 1 metr (m) = 1000 milimetrów (mm)
- 1 kilometr (km) = 1000 metrów (m)
- 1 centymetr (cm) = 10 milimetrów (mm)
Pamiętaj o tych przelicznikach, a zamiana jednostek długości stanie się dla Ciebie intuicyjna.
Gram, kilogram, tona: Opanuj przeliczanie masy bez wahania
Masa to kolejna podstawowa wielkość, z którą często mamy do czynienia. Oto jej kluczowe jednostki i przeliczniki:
- 1 kilogram (kg) = 100 dekagramów (dag)
- 1 kilogram (kg) = 1000 gramów (g)
- 1 dekagram (dag) = 10 gramów (g)
- 1 tona (t) = 1000 kilogramów (kg)
Te wartości są fundamentem do wszelkich obliczeń związanych z masą.
Praktyczne zadanie: Oblicz masę zakupów w gramach, znając ją w kilogramach
Załóżmy, że kupiłeś 2,5 kg owoców i chcesz wiedzieć, ile to gramów. Stosujemy nasz ułamek jednostkowy:
2,5 kg * (1000 g / 1 kg) = 2500 g
Twoje zakupy ważą 2500 gramów. Widzisz, jak proste to jest, gdy znasz przelicznik i metodę łańcuszkową?
Prędkość pod kontrolą: Przeliczanie km/h na m/s
Dlaczego dzielimy przez 3, 6? Odkrywamy tajemnicę przelicznika
Przeliczanie prędkości między kilometrami na godzinę (km/h) a metrami na sekundę (m/s) to jedno z tych zadań, które często sprawia problemy. Wielu uczniów pamięta magiczną liczbę 3,6, ale nie wie, skąd się ona bierze. Już tłumaczę! Współczynnik 3,6 wynika bezpośrednio z przeliczników długości i czasu:
- 1 kilometr (km) = 1000 metrów (m)
- 1 godzina (h) = 60 minut = 3600 sekund (s)
Jeśli chcemy zamienić km/h na m/s, robimy to tak:
1 km/h = (1 km / 1 h) = (1000 m / 3600 s) = (1000 / 3600) m/s = (10 / 36) m/s = (5 / 18) m/s
A jeśli chcemy zamienić m/s na km/h:
1 m/s = (1 m / 1 s) = (1/1000 km / 1/3600 h) = (3600 / 1000) km/h = 3,6 km/h
Dlatego właśnie pojawia się ta liczba 3,6! To nie żadna magia, tylko wynik podstawowych przeliczeń.
Kiedy mnożyć, a kiedy dzielić? Prosta zasada, by nigdy więcej się nie pomylić
Aby uniknąć pomyłek, zapamiętaj prostą zasadę:
- Jeśli przeliczasz z km/h na m/s (czyli z większej jednostki na mniejszą), dzielisz przez 3,6.
- Jeśli przeliczasz z m/s na km/h (czyli z mniejszej jednostki na większą), mnożysz przez 3,6.
Możesz też zawsze użyć metody łańcuszkowej, która jest niezawodna i pokaże Ci, co należy zrobić:
X km/h * (1000 m / 1 km) * (1 h / 3600 s) = X * (1000/3600) m/s = X / 3,6 m/s
Y m/s * (1 km / 1000 m) * (3600 s / 1 h) = Y * (3600/1000) km/h = Y * 3,6 km/h
Zadanie sprawdzające: Samochód jedzie 90 km/h. Jak szybko to jest w m/s?
Mamy prędkość 90 km/h i chcemy ją przeliczyć na m/s. Zgodnie z naszą zasadą, musimy podzielić przez 3,6:
90 km/h / 3,6 = 25 m/s
Samochód jedzie z prędkością 25 metrów na sekundę. To naprawdę proste, gdy zrozumiesz logikę!
Pole i objętość: Unikaj pułapek kwadratów i sześcianów
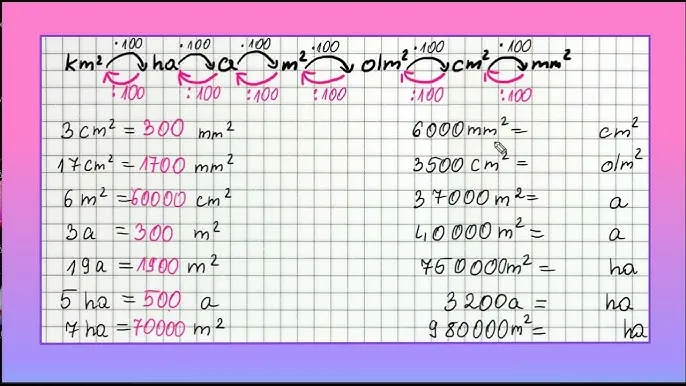
Dlaczego 1 m² to nie 100 cm²? Błąd, który popełnia prawie każdy
To jest jeden z najczęstszych błędów, jakie widzę u moich uczniów! Intuicja podpowiada, że skoro 1 metr to 100 centymetrów, to 1 metr kwadratowy powinien być równy 100 centymetrom kwadratowym. Niestety, to pułapka! Pamiętaj, że jednostka kwadratowa oznacza powierzchnię, czyli musimy podnieść do kwadratu nie tylko jednostkę, ale także jej przelicznik. Zobaczmy:
1 m = 100 cm
Jeśli podniesiemy obie strony do kwadratu, otrzymamy:
(1 m)² = (100 cm)²
1 m² = 100² cm²
1 m² = 10 000 cm²
To ogromna różnica! Zawsze pamiętaj o potęgowaniu przelicznika przy jednostkach powierzchni i objętości.
Hektary, ary, metry kwadratowe: Porządkujemy jednostki powierzchni
Oto najczęściej używane jednostki powierzchni i ich przeliczniki:
- 1 metr kwadratowy (m²) = 10 000 centymetrów kwadratowych (cm²)
- 1 ar (a) = 100 metrów kwadratowych (m²)
- 1 hektar (ha) = 100 arów (a)
- 1 hektar (ha) = 10 000 metrów kwadratowych (m²)
Te przeliczniki są kluczowe, zwłaszcza w zadaniach związanych z gruntami czy planowaniem przestrzennym.
Litry, metry sześcienne i mililitry: Zrozumieć relacje między jednostkami objętości
Objętość to kolejna wielkość, gdzie potęgi odgrywają kluczową rolę. Pamiętaj o tych relacjach:
- 1 metr sześcienny (m³) = 1 000 000 centymetrów sześciennych (cm³) (bo 1 m = 100 cm, więc 1 m³ = (100 cm)³ = 1 000 000 cm³)
- 1 litr (l) = 1 decymetr sześcienny (dm³)
- 1 litr (l) = 1000 mililitrów (ml)
- 1 litr (l) = 1000 centymetrów sześciennych (cm³)
- 1 mililitr (ml) = 1 centymetr sześcienny (cm³)
Zwróć uwagę na to, że litr jest równy decymetrowi sześciennemu to bardzo użyteczny przelicznik!
Ćwiczenie: Twoja wanna ma 0, 2 m³. Ile litrów wody pomieści?
Mamy objętość wanny 0,2 m³ i chcemy ją przeliczyć na litry. Wiemy, że 1 m³ = 1000 dm³ (bo 1 m = 10 dm, więc 1 m³ = (10 dm)³ = 1000 dm³), a 1 dm³ = 1 litr. Zatem:
0,2 m³ * (1000 dm³ / 1 m³) * (1 l / 1 dm³) = 200 l
Twoja wanna pomieści 200 litrów wody. To zadanie pokazuje, jak ważne jest łączenie różnych przeliczników.
Najczęstsze błędy i jak ich unikać: Twoja lista kontrolna
Błąd nr 1: Mnożenie zamiast dzielenia jak tego uniknąć?
To bardzo powszechny błąd, wynikający często z pośpiechu lub braku zrozumienia relacji między jednostkami. Czy mam pomnożyć, czy podzielić? To pytanie, które zadaje sobie wielu uczniów. Kluczem jest zawsze zastanowienie się, czy wynik powinien być większy, czy mniejszy od wartości początkowej. Jeśli przeliczasz z większej jednostki na mniejszą (np. kilometry na metry), wynik powinien być liczbowo większy, więc zazwyczaj mnożysz. Jeśli z mniejszej na większą (np. metry na kilometry), wynik powinien być liczbowo mniejszy, więc dzielisz. Metoda łańcuszkowa, z jej skracaniem jednostek, automatycznie prowadzi do prawidłowej operacji, eliminując ten problem.
Błąd nr 2: Ignorowanie potęg sekret kwadratów i sześcianów
Jak już wspomniałem, to prawdziwa pułapka! Zapominanie o podniesieniu przelicznika do kwadratu dla jednostek powierzchni (np. m² na cm²) lub do sześcianu dla jednostek objętości (np. m³ na cm³) to błąd, który kosztuje punkty na sprawdzianach. Zawsze, gdy widzisz jednostkę z potęgą (² lub ³), wiedz, że musisz zastosować tę samą potęgę do przelicznika! To prosta zasada, która uratuje Cię przed wieloma pomyłkami.
Przeczytaj również: Twierdzenie w fizyce: Klucz do zadań i zrozumienia zjawisk?
Błąd nr 3: Chaotyczny zapis dlaczego porządek na kartce to porządek w głowie?
Wiem, że czasem w ferworze walki z zadaniem łatwo o bałagan na kartce. Jednak chaotyczny zapis to prosta droga do pomyłek. Gdy obliczenia są rozrzucone, trudno jest śledzić tok rozumowania, a jeszcze trudniej znaleźć błąd. Staraj się pisać czytelnie, krok po kroku, wyraźnie zaznaczając, jakie jednostki się skracają. To nie tylko ułatwi Ci weryfikację własnych obliczeń, ale także pomoże nauczycielowi zrozumieć Twój tok myślenia i, co ważne, często pozwoli na zdobycie punktów nawet w przypadku drobnej pomyłki w końcowym wyniku.