Jak przekształcać wzory fizyka? Opanuj to krok po kroku!

Przekształcanie wzorów fizycznych to nic innego jak matematyczna gimnastyka, która pozwala nam "rozbroić" równanie i wyznaczyć dowolną niewiadomą. To umiejętność absolutnie kluczowa dla każdego ucznia, ponieważ otwiera drzwi do prawdziwego zrozumienia fizyki, zamiast tylko bezmyślnego zapamiętywania. W tym artykule pokażę Ci krok po kroku, jak opanować tę supermoc i zyskać pewność siebie w rozwiązywaniu nawet najbardziej podchwytliwych zadań.

Dlaczego przekształcanie wzorów to Twoja supermoc w fizyce?

Wielu uczniów patrzy na przekształcanie wzorów jak na jakąś skomplikowaną magię, dostępną tylko dla wybranych. Nic bardziej mylnego! Z mojego doświadczenia wiem, że to po prostu zestaw logicznych kroków, które każdy może opanować. Kiedy zrozumiesz, jak to działa, fizyka przestanie być zbiorem niezrozumiałych symboli, a stanie się fascynującym światem zależności. Opanowanie tej umiejętności to prawdziwa supermoc, która pozwoli Ci nie tylko zaliczyć sprawdzian, ale przede wszystkim zbudować solidne fundamenty do dalszej nauki i zyskać pewność siebie w obliczu każdego zadania.

Po co w ogóle przekształcać wzory? Odsłaniamy logikę fizyki

Zastanawiałeś się kiedyś, po co właściwie męczyć się z tymi wzorami? Odpowiedź jest prosta: przekształcanie wzorów pozwala nam wyznaczyć dowolną niewiadomą z danego równania. Wyobraź sobie, że masz wzór na prędkość, ale w zadaniu podana jest prędkość i czas, a musisz obliczyć drogę. Bez umiejętności przekształcania utknąłbyś. Co więcej, manipulowanie wzorami pogłębia Twoje zrozumienie fizyki. Zaczynasz dostrzegać, jak poszczególne wielkości fizyczne wpływają na siebie nawzajem, a to jest esencja nauki, a nie tylko sucha teoria. To klucz do prawdziwego zrozumienia zależności, a nie tylko do zapamiętywania.

Koniec z wkuwaniem na pamięć: jak jeden wzór daje wiele możliwości

Jedną z największych zalet umiejętności przekształcania wzorów jest to, że eliminuje ona potrzebę zapamiętywania dziesiątek różnych formuł. Wystarczy, że znasz jeden podstawowy wzór, a resztę możesz z niego "wyciągnąć". Weźmy na przykład klasyczny wzór na prędkość: v = s/t (prędkość to droga podzielona przez czas). Jeśli potrzebujesz wyznaczyć drogę (s), wystarczy pomnożyć obie strony przez 't', otrzymując s = v * t. A jeśli szukasz czasu (t)? Wtedy najpierw mnożymy obie strony przez 't', a następnie dzielimy przez 'v', co daje t = s/v. Widzisz? Z jednego wzoru masz trzy! To oszczędność czasu i energii, którą możesz poświęcić na zrozumienie problemu, a nie na bezmyślne wkuwanie.

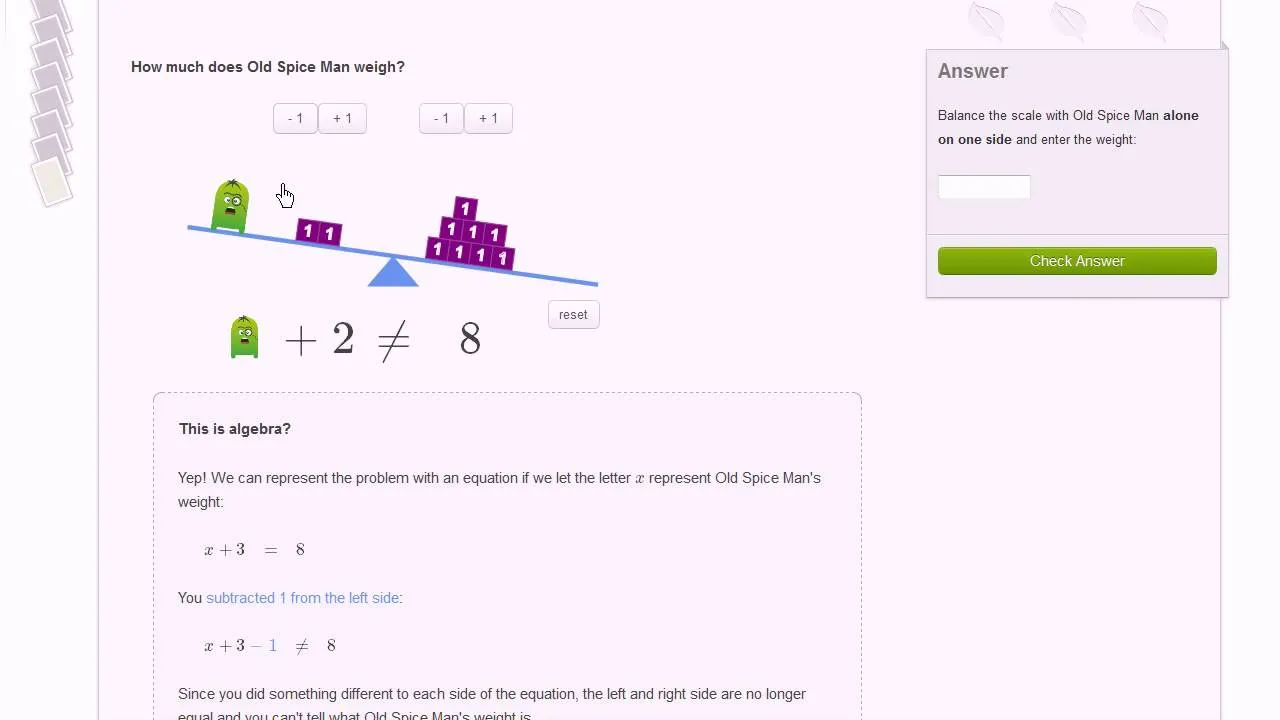
Matematyczne fundamenty: złote zasady, które musisz znać

Podstawą przekształcania wzorów jest prosta, ale niezwykle ważna zasada: równanie to jak waga, która musi pozostać w równowadze. Wyobraź sobie szalkową wagę, na której po obu stronach leżą odważniki. Jeśli coś dodasz, odejmiesz, pomnożysz lub podzielisz po jednej stronie, musisz zrobić dokładnie to samo po drugiej stronie, aby waga pozostała w równowadze, a równanie było nadal prawdziwe. To jest absolutnie fundamentalna zasada, której musisz się trzymać. Każda operacja, którą wykonujesz, musi objąć obie strony równania. To gwarantuje, że wynik będzie poprawny.

Działania przeciwne: Twoja tajna broń w porządkowaniu wzorów

Aby "uwolnić" szukaną wielkość z równania, stosujemy działania przeciwne. To Twoja tajna broń! Jeśli coś przeszkadza Twojej niewiadomej, użyj działania, które to "anuluje". Oto najważniejsze pary działań przeciwnych:

• Dodawanie i odejmowanie: Jeśli jakaś wielkość jest dodawana do szukanej zmiennej, odejmij ją od obu stron równania. Jeśli jest odejmowana, dodaj ją do obu stron.
• Mnożenie i dzielenie: Jeśli szukana zmienna jest mnożona przez jakąś wielkość, podziel obie strony równania przez tę wielkość. Jeśli jest dzielona, pomnóż obie strony przez tę wielkość.
• Potęgowanie i pierwiastkowanie: Jeśli szukana zmienna jest podniesiona do potęgi (np. do kwadratu), spierwiastkuj obie strony równania (np. pierwiastkiem kwadratowym). Jeśli zmienna jest pod pierwiastkiem, podnieś obie strony równania do odpowiedniej potęgi.

Kolejność działań: poznaj hierarchię, która rządzi w matematyce

W standardowych obliczeniach pamiętamy o kolejności: najpierw nawiasy, potem potęgi, następnie mnożenie/dzielenie, a na końcu dodawanie/odejmowanie. Przy przekształcaniu wzorów działamy... odwrotnie! To bardzo ważna zasada, której nieprzestrzeganie jest częstą przyczyną błędów. Najpierw "pozbywamy się" tego, co jest najdalej od naszej szukanej zmiennej, czyli operacji dodawania i odejmowania, a dopiero potem mnożenia i dzielenia, a na końcu potęg i pierwiastków. Pamiętaj o tej hierarchii, a unikniesz wielu pułapek:

1. Dodawanie i odejmowanie
2. Mnożenie i dzielenie
3. Potęgowanie i pierwiastkowanie
4. Nawiasy (jeśli występują i nie da się ich wcześniej uprościć)

Przekształcanie wzorów krok po kroku: prosta metoda, która zawsze działa

Krok 1: Określ cel którą wielkość chcesz "uratować" z równania?

Zanim zaczniesz cokolwiek robić, musisz jasno określić, którą zmienną chcesz wyznaczyć. To jest Twój cel, Twoja "misja". Zaznacz ją sobie w myślach, zakreśl na kartce, zrób cokolwiek, byś zawsze wiedział, do czego dążysz. To klucz do skutecznego działania, bo pozwala skupić się na właściwych operacjach i nie zgubić się w gąszczu symboli.

Krok 2: Pozbądź się ułamków i nawiasów uprość sobie pole bitwy

Ułamki i nawiasy często utrudniają życie, więc najlepiej pozbyć się ich na początku. Jeśli masz ułamek, pomnóż obie strony równania przez mianownik, aby go usunąć. Pamiętaj, aby pomnożyć CAŁĄ drugą stronę! Jeśli masz nawiasy, rozdziel czynniki, czyli pomnóż wszystko w nawiasie przez to, co stoi przed nim. To uprości równanie i sprawi, że dalsze kroki będą łatwiejsze.

Przykład (ułamek): Jeśli masz F = m/a i chcesz wyznaczyć 'a', pomnóż obie strony przez 'a': F * a = m.

Przykład (nawias): Jeśli masz P = 2(a+b) i chcesz wyznaczyć 'a', najpierw rozdziel: P = 2a + 2b.

Krok 3: Przerzucaj wyrazy na drugą stronę czyli o dodawaniu i odejmowaniu

Teraz czas na dodawanie i odejmowanie. Wszystkie wyrazy, które są dodawane lub odejmowane od Twojej szukanej zmiennej, "przerzuć" na drugą stronę równania. Pamiętaj o złotej zasadzie: zawsze zmieniaj znak na przeciwny! Jeśli coś było dodawane (+), stanie się odejmowane (-). Jeśli było odejmowane (-), stanie się dodawane (+). To uproszczenie myślowe "przenoszenia na drugą stronę ze zmianą znaku" jest bardzo pomocne i szybko wchodzi w krew.

Przykład: Jeśli masz E = mgh + Ek i chcesz wyznaczyć 'mgh', odejmij 'Ek' od obu stron: E - Ek = mgh.

Krok 4: Uwolnij swoją niewiadomą od mnożenia i dzielenia

Gdy już pozbyłeś się dodawania i odejmowania, przyszedł czas na mnożenie i dzielenie. Jeśli Twoja szukana zmienna jest mnożona przez inną wielkość, podziel obie strony równania przez tę wielkość. Jeśli jest dzielona, pomnóż obie strony przez nią. Dzięki temu Twoja niewiadoma zostanie sama po jednej stronie równania.

Przykład: Jeśli masz F = m * a i chcesz wyznaczyć 'a', podziel obie strony przez 'm': F/m = a.

Krok 5: Co zrobić z potęgą lub pierwiastkiem? Ostatni etap operacji

Na koniec, jeśli Twoja szukana zmienna jest podniesiona do potęgi (np. do kwadratu), musisz spierwiastkować obie strony równania odpowiednim pierwiastkiem. Jeśli natomiast zmienna jest pod pierwiastkiem, podnieś obie strony równania do odpowiedniej potęgi. Pamiętaj, aby pierwiastkować lub potęgować CAŁĄ drugą stronę równania, a nie tylko jej fragment!

Przykład: Jeśli masz Ek = (m * v²) / 2 i chcesz wyznaczyć 'v', po wcześniejszych przekształceniach dojdziesz do 2Ek / m = v². Wtedy spierwiastkuj obie strony: √(2Ek / m) = v.

Przykłady z lekcji fizyki: zobacz, jak to działa w praktyce

Przykład dla początkujących: Jak ze wzoru na gęstość (d=m/V) wyliczyć masę?

1. Wzór początkowy: d = m/V (gdzie 'd' to gęstość, 'm' to masa, 'V' to objętość).
2. Cel: Chcemy wyznaczyć masę 'm'.
3. Krok 1 (pozbycie się ułamka): Zmienna 'm' jest dzielona przez 'V'. Aby się pozbyć 'V' z mianownika, mnożymy obie strony równania przez 'V'. d * V = (m/V) * V d * V = m
4. Wynik: Otrzymaliśmy wzór na masę: m = d * V. Proste, prawda?

Klasyk z lekcji fizyki: Wyznaczanie przyspieszenia (a) z II zasady dynamiki Newtona (F=m*a)

1. Wzór początkowy: F = m * a (gdzie 'F' to siła, 'm' to masa, 'a' to przyspieszenie).
2. Cel: Chcemy wyznaczyć przyspieszenie 'a'.
3. Krok 1 (uwolnienie od mnożenia): Zmienna 'a' jest mnożona przez 'm'. Aby ją "uwolnić", musimy podzielić obie strony równania przez 'm'. F / m = (m * a) / m F / m = a
4. Wynik: Otrzymaliśmy wzór na przyspieszenie: a = F / m.

Wyższy poziom trudności: Jak wyznaczyć prędkość (v) ze wzoru na energię kinetyczną (Ek = mv²/2)?

1. Wzór początkowy: Ek = (m * v²) / 2 (gdzie 'Ek' to energia kinetyczna, 'm' to masa, 'v' to prędkość).
2. Cel: Chcemy wyznaczyć prędkość 'v'.
3. Krok 1 (pozbycie się ułamka): Zmienna 'v' jest w ułamku. Mnożymy obie strony przez mianownik (2): Ek * 2 = (m * v² / 2) * 2 2Ek = m * v²
4. Krok 2 (uwolnienie od mnożenia): Zmienna 'v²' jest mnożona przez 'm'. Dzielimy obie strony przez 'm': 2Ek / m = (m * v²) / m 2Ek / m = v²
5. Krok 3 (pozbycie się potęgi): Zmienna 'v' jest podniesiona do kwadratu. Pierwiastkujemy obie strony równania: √(2Ek / m) = √v² √(2Ek / m) = v
6. Wynik: Otrzymaliśmy wzór na prędkość: v = √(2Ek / m).

Najczęstsze błędy w przekształcaniu wzorów i jak ich unikać

Pułapka nr 1: Mianownik ułamka jak poprawnie się go pozbyć?

Bardzo częstym błędem jest niepoprawne pozbywanie się mianownika. Jeśli masz równanie, np. A = B/C + D i chcesz wyznaczyć 'B', a zaczniesz od pomnożenia tylko B/C przez 'C', to popełnisz błąd. Pamiętaj, że mnożysz CAŁĄ drugą stronę! Czyli prawidłowo byłoby: A * C = (B/C + D) * C, co daje A * C = B + D * C. Dopiero wtedy możesz dalej operować.

Błędnie: A = B/C + D -> A * C = B + D (zapomniano pomnożyć D przez C)

Poprawnie: A = B/C + D -> A * C = B + D * C

Pułapka nr 2: "Zapomniany" minus gubienie znaków przy przenoszeniu

To klasyka! Kiedy przenosisz wyraz na drugą stronę równania, musisz zmienić jego znak. Jeśli masz X - Y = Z i chcesz wyznaczyć 'X', to przenosząc 'Y' na drugą stronę, często zapomina się o zmianie znaku. Prawidłowo powinno być X = Z + Y, a nie X = Z - Y. Zawsze dokładnie sprawdzaj znaki!

Przykład: 5 - x = 2. Aby wyznaczyć 'x', przenosimy '5': -x = 2 - 5, czyli -x = -3. Dopiero teraz mnożymy przez -1: x = 3.

Pułapka nr 3: Potęga dotyczy tylko jednej litery? Błąd, którego musisz unikać

Kiedy pierwiastkujesz lub podnosisz do potęgi obie strony równania, ta operacja musi objąć CAŁĄ drugą stronę. Jeśli masz A² = B + C i chcesz wyznaczyć 'A', to prawidłowo jest A = √(B + C), a nie A = √B + √C. Pierwiastek obejmuje całą sumę! To samo dotyczy potęgowania. Bądź bardzo ostrożny z zasięgiem tych operacji.

Błędnie: v² = 2Ek / m -> v = √2Ek / √m

Poprawnie: v² = 2Ek / m -> v = √(2Ek / m)

Pułapka nr 4: Zła kolejność dlaczego najpierw pozbywamy się dodawania, a potem mnożenia?

Jak już wspomniałem, przy przekształcaniu wzorów działamy odwrotnie niż przy zwykłych obliczeniach. Najpierw "rozplątujemy" dodawanie i odejmowanie, a dopiero potem mnożenie i dzielenie. Wyobraź sobie, że zmienna jest "opakowana" w działania. Musisz zdjąć te "opakowania" w odwrotnej kolejności. Nieprzestrzeganie tego prowadzi do błędów. Na przykład, jeśli masz F = m * a + b i chcesz wyznaczyć 'a', nie możesz od razu dzielić przez 'm'. Najpierw musisz odjąć 'b' od obu stron: F - b = m * a, a dopiero potem podzielić przez 'm': (F - b) / m = a.

Jak ćwiczyć, żeby stać się mistrzem przekształcania wzorów?

Zacznij od prostych wzorów i stopniowo podnoś poprzeczkę

Nie rzucaj się od razu na głęboką wodę! Zacznij od najprostszych wzorów, takich jak te na gęstość (d=m/V), prędkość (v=s/t) czy drugą zasadę dynamiki Newtona (F=m*a). Kiedy poczujesz się pewnie, przejdź do bardziej złożonych, np. na energię kinetyczną (Ek = mv²/2) czy prawo Ohma (U=I*R). Regularne ćwiczenia to klucz do sukcesu. Im więcej przekształcisz, tym szybciej i pewniej będziesz to robić.

Nie tylko przekształcaj zawsze sprawdzaj jednostki!

To jest złota zasada, którą zawsze powtarzam moim uczniom! Po każdym przekształceniu wzoru, sprawdź jednostki. Jeśli wyznaczasz prędkość (v) i w Twoim przekształconym wzorze po prawej stronie wyjdzie Ci jednostka metra (m) zamiast metra na sekundę (m/s), to wiesz, że gdzieś popełniłeś błąd. Zgodność jednostek jest potężnym narzędziem weryfikacji i często pozwala wyłapać błędy, zanim jeszcze zaczniesz podstawiać liczby.

Przeczytaj również: Fizyka matura: 180 min. Strategie, arkusz, przybory Twój sukces!

Stwórz własną "ściągę" z przekształconymi najważniejszymi wzorami

Kiedy już opanujesz przekształcanie najczęściej używanych wzorów, stwórz sobie osobisty notatnik lub "ściągę". Zapisz w nim podstawowy wzór, a następnie jego przekształcone wersje dla każdej zmiennej. Na przykład: v = s/t s = v*t t = s/v Takie zestawienie będzie świetną pomocą podczas rozwiązywania zadań, a proces jego tworzenia dodatkowo utrwali Twoją wiedzę. Pamiętaj, że to nie jest "ściąga" w złym tego słowa znaczeniu, ale narzędzie do nauki i utrwalania!