Wielu uczniów uważa fizykę za przedmiot trudny, a jednym z największych wyzwań jest dla nich przekształcanie wzorów. Jeśli szukasz praktycznego przewodnika, który krok po kroku wyjaśni Ci, jak manipulować równaniami fizycznymi, aby wyizolować konkretną zmienną, to dobrze trafiłeś. W tym artykule pokażę Ci sprawdzone metody i triki, dzięki którym opanowanie tej kluczowej umiejętności stanie się znacznie prostsze.
Przekształcanie wzorów z fizyki to umiejętność do opanowania poznaj proste zasady i kroki
- Kluczem do przekształcania wzorów jest wykonywanie tych samych operacji po obu stronach równania, aby zachować jego prawdziwość.
- Przestrzegaj kolejności działań matematycznych, tak jak przy rozwiązywaniu równań algebraicznych.
- Stosuj uniwersalną metodę krok po kroku: usuń mianowniki, przenieś niewiadome, wyłącz wspólny czynnik, a następnie podziel.
- Uważaj na najczęstsze błędy, takie jak gubienie znaków, mylenie operacji mnożenia z dzieleniem czy pomijanie jednostek.
- Dla prostych wzorów z trzema zmiennymi pomocny może być "magiczny trójkąt", ułatwiający szybkie przekształcenia.
- Biegłość w przekształcaniu wzorów zdobywa się poprzez regularne ćwiczenia na różnorodnych przykładach.
Po co w ogóle przekształcać wzory? Odkryj klucz do rozwiązywania zadań
Z mojego doświadczenia wiem, że umiejętność przekształcania wzorów to absolutny fundament w fizyce. Bez niej rozwiązywanie zadań obliczeniowych staje się niemożliwe, bo rzadko kiedy dane są podane w idealnej kolejności, by od razu podstawić je do wzoru. To właśnie ta umiejętność pozwala nam dostosować wzór do potrzeb konkretnego zadania, wyznaczając szukaną wielkość, niezależnie od tego, czy jest to prędkość, masa, czy czas. Dla uczniów to klucz do zrozumienia, jak działa świat fizyki i jak "rozmawiać" z liczbami.Odblokuj swój potencjał: Jak ta jedna umiejętność zmienia wszystko na fizyce
Opanowanie przekształcania wzorów to prawdziwy game changer. Widziałem, jak moi uczniowie, którzy początkowo bali się fizyki, nagle zyskują pewność siebie, gdy tylko zrozumieją, jak swobodnie operować równaniami. To nie tylko ułatwia codzienne lekcje, ale jest także absolutnie niezbędne do sukcesu na egzaminach, takich jak egzamin ósmoklasisty czy matura. Bez tej biegłości, nawet najlepsza znajomość teorii nie pomoże w zdobyciu punktów za zadania obliczeniowe. To umiejętność, która naprawdę otwiera drzwi do zrozumienia fizyki.

Złote zasady przekształcania równań fizycznych
Zasada nr 1: Traktuj obie strony równania jednakowo
To jest absolutna podstawa i zasada numer jeden, którą zawsze powtarzam moim uczniom: cokolwiek robisz z jedną stroną równania, musisz zrobić z drugą. Jeśli dodajesz jakąś wartość po lewej stronie, musisz dodać ją również po prawej. Jeśli mnożysz przez coś lewą stronę, prawa strona również musi być przez to pomnożona. Tylko w ten sposób zachowasz równowagę i prawdziwość równania, a co za tym idzie poprawność przekształcenia.
Operacje matematyczne jako Twoje narzędzia: Kiedy dodawać, a kiedy mnożyć?
Podstawowe operacje matematyczne to Twoje narzędzia do izolowania szukanej zmiennej. Pamiętaj, że zawsze dążymy do "rozdzielenia" szukanej wielkości od reszty. Jeśli szukana zmienna jest połączona z inną wielkością za pomocą dodawania, użyj odejmowania, aby ją przenieść. Jeśli jest połączona mnożeniem, użyj dzielenia. To prosta zasada: zawsze stosuj operację odwrotną do tej, która łączy szukaną zmienną z innymi elementami wzoru. Na przykład, jeśli masz `x + y = z` i szukasz `x`, odejmij `y` od obu stron.
Rola kolejności działań: Dlaczego jest tak ważna i jak jej pilnować?
Kolejność działań matematycznych, czyli słynne "PEMDAS" (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) lub polskie "kolejność wykonywania działań", jest równie ważna przy przekształcaniu wzorów, jak przy rozwiązywaniu zwykłych równań algebraicznych. Zawsze najpierw zajmuj się nawiasami i potęgami, potem mnożeniem i dzieleniem, a na końcu dodawaniem i odejmowaniem. Ignorowanie tej kolejności to jeden z najczęstszych błędów, który prowadzi do całkowicie błędnych wyników. Traktuj wzory fizyczne jak skomplikowane równania zasady są te same.
Uniwersalna metoda przekształcania wzorów krok po kroku
Przekształcanie wzorów nie musi być chaotyczne. Opracowałem uniwersalną metodę, która składa się z kilku prostych kroków. Stosując ją systematycznie, poradzisz sobie z większością równań, niezależnie od ich złożoności. To podejście zapewni Ci porządek i minimalizuje ryzyko pomyłek.
Krok 1: Pozbądź się mianowników Twój pierwszy ruch w stronę prostszego wzoru
Pierwszym krokiem, który zawsze polecam, jest usunięcie wszystkich mianowników. Ułamki często komplikują sprawę i wprowadzają niepotrzebne zamieszanie. Aby się ich pozbyć, pomnóż obie strony równania przez wspólny mianownik wszystkich ułamków. Jeśli masz tylko jeden ułamek, pomnóż przez jego mianownik. Dzięki temu równanie stanie się liniowe i znacznie łatwiejsze do dalszej manipulacji.
Krok 2: Uporządkuj niewiadome przenieś szukaną wielkość na lewą stronę
Gdy już pozbędziesz się mianowników, czas na uporządkowanie. Przenieś wszystkie wyrazy zawierające szukaną niewiadomą na jedną stronę równania (zazwyczaj lewą), a wszystkie pozostałe wyrazy na drugą stronę (prawą). Pamiętaj o bardzo ważnej zasadzie: przy przenoszeniu wyrazu na drugą stronę równania zawsze zmieniamy jego znak na przeciwny. Czyli z plusa robi się minus, a z minusa plus.
Krok 3: Wyłącz wspólny czynnik przed nawias technika dla bardziej złożonych wzorów
Ten krok jest kluczowy w bardziej złożonych wzorach, gdzie szukana niewiadoma występuje w kilku wyrazach po tej samej stronie równania. W takiej sytuacji wyłącz szukaną niewiadomą przed nawias. W nawiasie pozostanie suma lub różnica pozostałych współczynników i zmiennych. To pozwoli Ci "zebrać" wszystkie wystąpienia szukanej wielkości w jedno miejsce, co jest niezbędne do jej ostatecznego wyizolowania.
Krok 4: Finałowe dzielenie jak wyizolować szukaną zmienną?
To ostatni, decydujący krok. Po wykonaniu poprzednich operacji, po jednej stronie równania powinieneś mieć szukaną niewiadomą pomnożoną przez jakiś współczynnik (lub wyrażenie w nawiasie), a po drugiej stronie resztę równania. Aby całkowicie wyizolować szukaną zmienną, podziel obie strony równania przez to, co "stoi" przy niewiadomej. W ten sposób uzyskasz wzór, w którym szukana wielkość jest sama po jednej stronie, a reszta po drugiej.
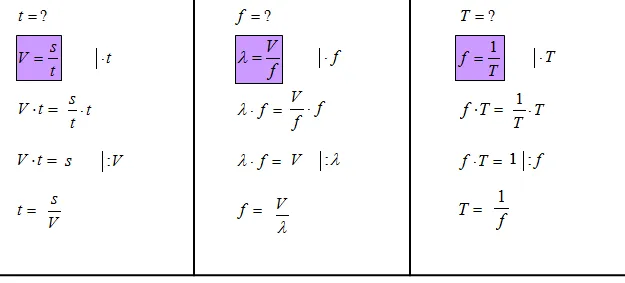
Przykłady w praktyce: Przekształcanie popularnych wzorów
Teoria to jedno, ale prawdziwe zrozumienie przychodzi z praktyką. Pokażę Ci teraz, jak zastosować omówione zasady i metodę "krok po kroku" na najczęściej spotykanych wzorach fizycznych. Zobaczysz, że z odpowiednim podejściem, nawet skomplikowane na pierwszy rzut oka wzory stają się proste do przekształcenia.
Przykład 1: Wzór na prędkość (v = s/t) jak obliczyć drogę i czas?
Zacznijmy od klasyki: wzoru na prędkość. Mamy `v = s/t` (prędkość = droga / czas).
Wyznaczenie drogi (s):
- Mamy wzór: `v = s/t`
- Aby pozbyć się mianownika `t`, mnożymy obie strony przez `t`: `v * t = (s/t) * t`
- Po uproszczeniu otrzymujemy: `s = v * t`
Wyznaczenie czasu (t):
- Mamy wzór: `v = s/t`
- Mnożymy obie strony przez `t` (jak wyżej): `v * t = s`
- Teraz chcemy wyizolować `t`. Dzielimy obie strony przez `v`: `(v * t) / v = s / v`
- Po uproszczeniu otrzymujemy: `t = s / v`
Przykład 2: Energia potencjalna (Ep = mgh) jak wyznaczyć masę lub wysokość?
Wzór na energię potencjalną to `Ep = m * g * h` (energia potencjalna = masa * przyspieszenie ziemskie * wysokość).Wyznaczenie masy (m):
- Mamy wzór: `Ep = m * g * h`
- Szukamy `m`. Widzimy, że `m` jest pomnożone przez `g` i `h`.
- Aby wyizolować `m`, dzielimy obie strony przez `g * h`: `Ep / (g * h) = (m * g * h) / (g * h)`
- Po uproszczeniu otrzymujemy: `m = Ep / (g * h)`
Wyznaczenie wysokości (h):
- Mamy wzór: `Ep = m * g * h`
- Szukamy `h`. Widzimy, że `h` jest pomnożone przez `m` i `g`.
- Aby wyizolować `h`, dzielimy obie strony przez `m * g`: `Ep / (m * g) = (m * g * h) / (m * g)`
- Po uproszczeniu otrzymujemy: `h = Ep / (m * g)`
Przykład 3: II zasada dynamiki (F = m*a) jak obliczyć przyspieszenie?
Druga zasada dynamiki Newtona to `F = m * a` (siła = masa * przyspieszenie).Wyznaczenie przyspieszenia (a):
- Mamy wzór: `F = m * a`
- Szukamy `a`. Widzimy, że `a` jest pomnożone przez `m`.
- Aby wyizolować `a`, dzielimy obie strony przez `m`: `F / m = (m * a) / m`
- Po uproszczeniu otrzymujemy: `a = F / m`
Najczęstsze błędy przy przekształcaniu wzorów i jak ich unikać
W mojej praktyce widziałem wiele błędów popełnianych przez uczniów, ale dobra wiadomość jest taka, że większość z nich jest powtarzalna i łatwa do uniknięcia, jeśli tylko wiesz, na co uważać. Znajomość tych pułapek to już połowa sukcesu, bo pozwala świadomie kontrolować swoje działania i nie tracić niepotrzebnie punktów.
Pułapka nr 1: Gubienie znaków przy przenoszeniu jak tego uniknąć?
To chyba najczęstszy błąd! Uczniowie często zapominają o zmianie znaku (+/-) przy przenoszeniu wyrazu na drugą stronę równania. Na przykład, jeśli masz `A + B = C` i chcesz wyznaczyć `A`, powinieneś przenieść `B` na prawą stronę, zmieniając jego znak na minus: `A = C - B`. Często widzę, jak zostaje `A = C + B`, co jest oczywiście błędem. Aby tego uniknąć, zawsze po przeniesieniu wyrazu, sprawdź dwukrotnie, czy zmieniłeś jego znak. To prosta, ale skuteczna metoda.
Pułapka nr 2: Mylenie mnożenia z dzieleniem prosty sposób na weryfikację
Inny powszechny błąd to mylenie operacji mnożenia z dzieleniem. Jeśli szukana zmienna jest pomnożona przez inną wielkość, aby ją wyizolować, musisz podzielić obie strony równania przez tę wielkość. I odwrotnie, jeśli zmienna jest dzielona, musisz pomnożyć. Prosty sposób na weryfikację: wyobraź sobie, że masz prosty wzór, np. `6 = 2 * 3`. Jeśli chcesz wyznaczyć `2`, musisz podzielić `6` przez `3`. Jeśli chcesz wyznaczyć `3`, musisz podzielić `6` przez `2`. To pomaga zapamiętać, kiedy stosować którą operację.
Pułapka nr 3: Zapominanie o jednostkach dlaczego to krytyczny błąd?
Kontrolowanie jednostek to nie tylko formalność, ale kluczowy element weryfikacji poprawności Twoich obliczeń. Jeśli w wyniku przekształcenia wzoru na prędkość otrzymasz wzór, który po podstawieniu jednostek daje Ci metry na sekundę (m/s), to jest dobrze. Ale jeśli dostaniesz metry razy sekundy (m*s), to wiesz, że gdzieś popełniłeś błąd. Zapominanie o jednostkach lub ich błędne stosowanie to krytyczny błąd, który nie tylko prowadzi do niepoprawnych wyników, ale także świadczy o braku zrozumienia fizycznego sensu wzoru. Zawsze sprawdzaj jednostki na każdym etapie to jak wbudowany system kontroli jakości.
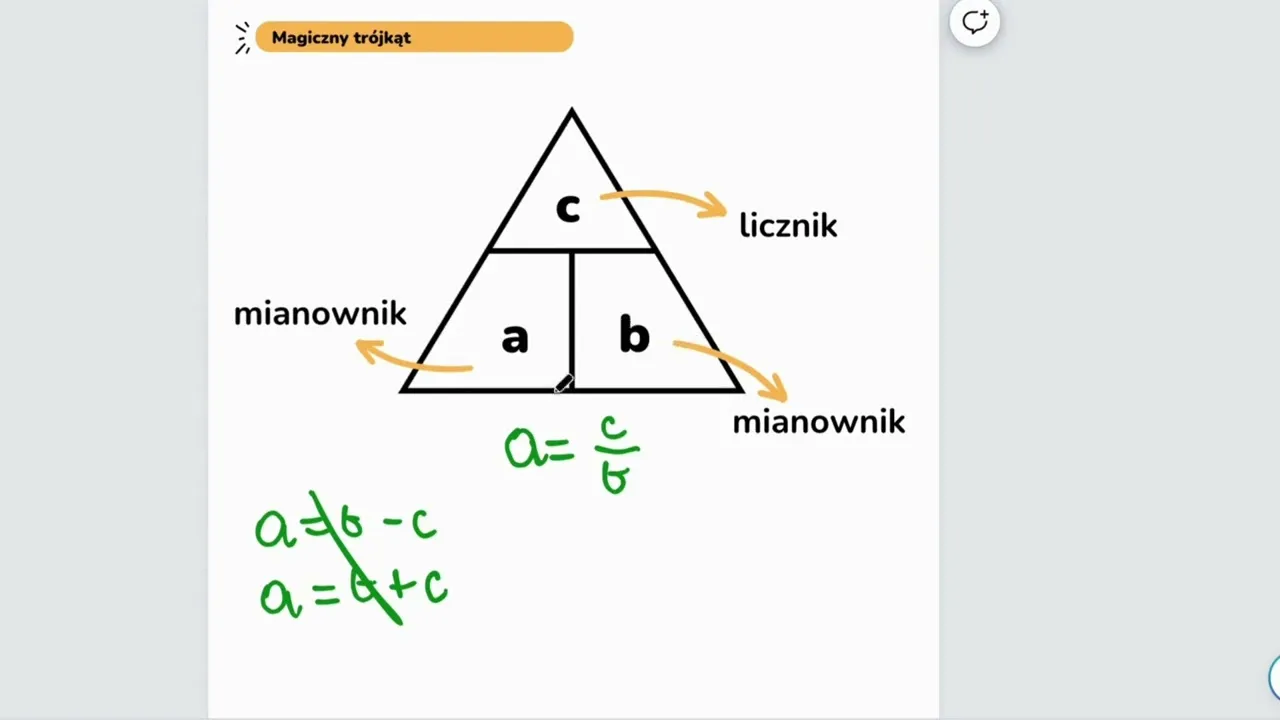
Proste triki wizualne ułatwiające przekształcanie wzorów
Magiczny trójkąt: Jak go używać dla wzorów z trzema zmiennymi?
Dla prostych wzorów z trzema zmiennymi, takich jak `v = s/t` (prędkość, droga, czas) czy `F = m*a` (siła, masa, przyspieszenie), istnieje świetna pomoc wizualna "magiczny trójkąt". Rysujesz trójkąt i dzielisz go na trzy części: jedną na górze i dwie na dole. Na górze umieszczasz zmienną, która jest wynikiem mnożenia dwóch pozostałych (np. `s` w `s = v*t`). Na dole umieszczasz pozostałe dwie zmienne. Aby wyznaczyć szukaną zmienną, po prostu zakryj ją palcem. Pozostałe zmienne pokażą Ci, jaką operację należy wykonać. Jeśli są obok siebie, mnożysz je; jeśli jedna jest nad drugą, dzielisz.
Kiedy warto stosować metody wizualne, a kiedy lepiej zaufać algebrze?
Magiczny trójkąt to fantastyczne narzędzie do szybkiego przekształcania prostych wzorów, szczególnie na początku nauki. Jest intuicyjny i minimalizuje ryzyko pomyłek w podstawowych przypadkach. Jednakże, gdy wzory stają się bardziej złożone, zawierają dodawanie, odejmowanie, nawiasy, potęgi czy pierwiastki, metody algebraiczne stają się niezastąpione. Trójkąt przestaje być wtedy wystarczający. Moją radą jest: zacznij od trójkąta, aby zbudować pewność siebie, ale równocześnie rozwijaj umiejętności algebraiczne, które pozwolą Ci na radzenie sobie z każdym wyzwaniem.
Jak skutecznie ćwiczyć, by opanować przekształcanie wzorów?
Od czego zacząć? Proste ćwiczenia na rozgrzewkę
- Zacznij od najprostszych wzorów: Takich jak `v = s/t`, `F = m*a`, `P = U*I`. Skup się na ich przekształcaniu w celu wyznaczenia każdej zmiennej.
- Pracuj systematycznie: Nie rzucaj się od razu na skomplikowane równania. Stopniowo zwiększaj poziom trudności, dodając wzory z dodawaniem/odejmowaniem, a następnie te z nawiasami.
- Użyj kartek i długopisu: Aktywne pisanie pomaga w zapamiętywaniu i utrwalaniu schematów myślowych. Nie tylko patrz na rozwiązania, ale sam je twórz.
Zwiększamy trudność: Gdzie szukać zadań i jak sprawdzać swoje wyniki?
- Podręczniki i zbiory zadań: Są kopalnią przykładów i zadań do ćwiczeń. Często zawierają też rozwiązania, co pozwala na bieżące sprawdzanie poprawności.
- Materiały online: Wiele stron internetowych i kanałów YouTube oferuje dodatkowe zadania i szczegółowe wyjaśnienia. Szukaj "zadania z przekształcania wzorów fizyka".
- Sprawdzaj swoje wyniki: Po przekształceniu wzoru, podstaw do niego proste liczby, a następnie sprawdź, czy wynik zgadza się z tym, co otrzymałbyś, podstawiając te same liczby do oryginalnego wzoru. To niezawodna metoda weryfikacji.
Przeczytaj również: Fizyka w szkole: Od kiedy, co w programie i zmiany 2026?
Regularność to klucz: Jak wpleść ćwiczenia w codzienną naukę?
Jak w każdej umiejętności, tak i w przekształcaniu wzorów, regularność jest absolutnie kluczowa. Zamiast uczyć się na ostatnią chwilę, poświęć 10-15 minut każdego dnia na przekształcanie 2-3 wzorów. Możesz to robić przed odrabianiem lekcji z fizyki, albo jako krótką "rozgrzewkę" umysłową. Dzięki temu schematy działania utrwalą się w Twojej pamięci, a sama czynność stanie się intuicyjna. Pamiętaj, że mistrzostwo osiąga się poprzez konsekwentną praktykę, a nie jednorazowe zrywy.

